Systems of Equations

TME 310 - Computational Physical Modeling

Lorne Arnold, PhD, PE

University of Washington Tacoma

Systems of equations

\[ x + 3y + 4z = 8\\ 4x - 2y + 8z = -4\\ -x + 4y + z = 12 \]

Solve for \(x\), \(y\), and \(z\)

We can solve any system of equations as long as…

The number of equations is \(\geq\) the number of unknowns
The equations are linearly independent

Solving systems of equations

In algebra, we learned different methods to solve for unknowns.

Graphing
Substitution
Elimination
Guess and check?

We’ll use matrices and concepts from linear algebra to get Python to solve systems of equations for us.

Matrix form

First, we need to put our system of equations into matrix form:

\[A\bf{x} = \bf{b}\]

Coefficients matrix, \(A\)
Unknowns vector, \(\bf{x}\)
Constants vector, \(\bf{b}\)

\[ \begin{bmatrix} a_{11} & a_{12} & a_{13}\\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \\ \end{bmatrix} \times \begin{bmatrix} x_{11}\\ x_{21}\\ x_{31}\\ \end{bmatrix} = \begin{bmatrix} b_{11}\\ b_{21}\\ b_{31}\\ \end{bmatrix} \]

System of equations example

\[ x + 3y + 4z = 8\\ 4x - 2y + 8z = -4\\ -x + 4y + z = 12 \]

\[ A= \begin{bmatrix} 1 & 3 & 4\\ 4 & -2 & 8 \\ -1 & 4 & 1 \\ \end{bmatrix} \]

\[ {\bf{x}} \to \begin{bmatrix} x\\ y\\ z\\ \end{bmatrix} \]

\[ {\bf{b}} \to \begin{bmatrix} 8\\ -4\\ 12\\ \end{bmatrix} \]

System of equations example

\[ x + 3y + 4z = 8\\ 4x - 2y + 8z = -4\\ -x + 4y + z = 12 \]

\[ \begin{bmatrix} 1 & 3 & 4\\ 4 & -2 & 8 \\ -1 & 4 & 1 \\ \end{bmatrix} \times \begin{bmatrix} x\\ y\\ z\\ \end{bmatrix} = \begin{bmatrix} 8\\ -4\\ 12\\ \end{bmatrix} \]

Solving

To solve for \(\bf{x}\), we “divide” both sides by \(A\) (i.e., multiply both sides by \(A^{-1}\)):

\[A{\bf{x}} = \bf{b}\]

\[A^{-1}A{\bf{x}} = A^{-1}\bf{b}\]

\[I{\bf{x}} = A^{-1}\bf{b}\]

\[{\bf{x}} = A^{-1}\bf{b}\]

Solved in Python

import numpy as np
from scipy import linalg
A = np.array([
    [1, 3, 4], 
    [4, -2, 8],
    [-1, -4, 1]])
b = np.array([
    [8], 
    [-4],
    [2]])
# A@x = b --> x = A_inv@b
x = linalg.inv(A) @ b 
# Or use the "solve" function:
# x = linalg.solve(A, b) 
print(x)

[[-4.87179487]
 [ 1.28205128]
 [ 2.25641026]]

print(A@x)

[[ 8.]
 [-4.]
 [ 2.]]

Linear independence?

What about the requirement that the equations in our system are “linearly independent”?

The coefficients matrix (\(A\)) will have a non-zero determinant if the system is linearly independent.

linalg.det(A)

np.float64(-78.0)

A = np.array([
    [1, 3, 4], 
    [4, -2, 8],
    [8, -4, 16]])
linalg.det(A)
# A is "singular"

np.float64(0.0)

Engineering example

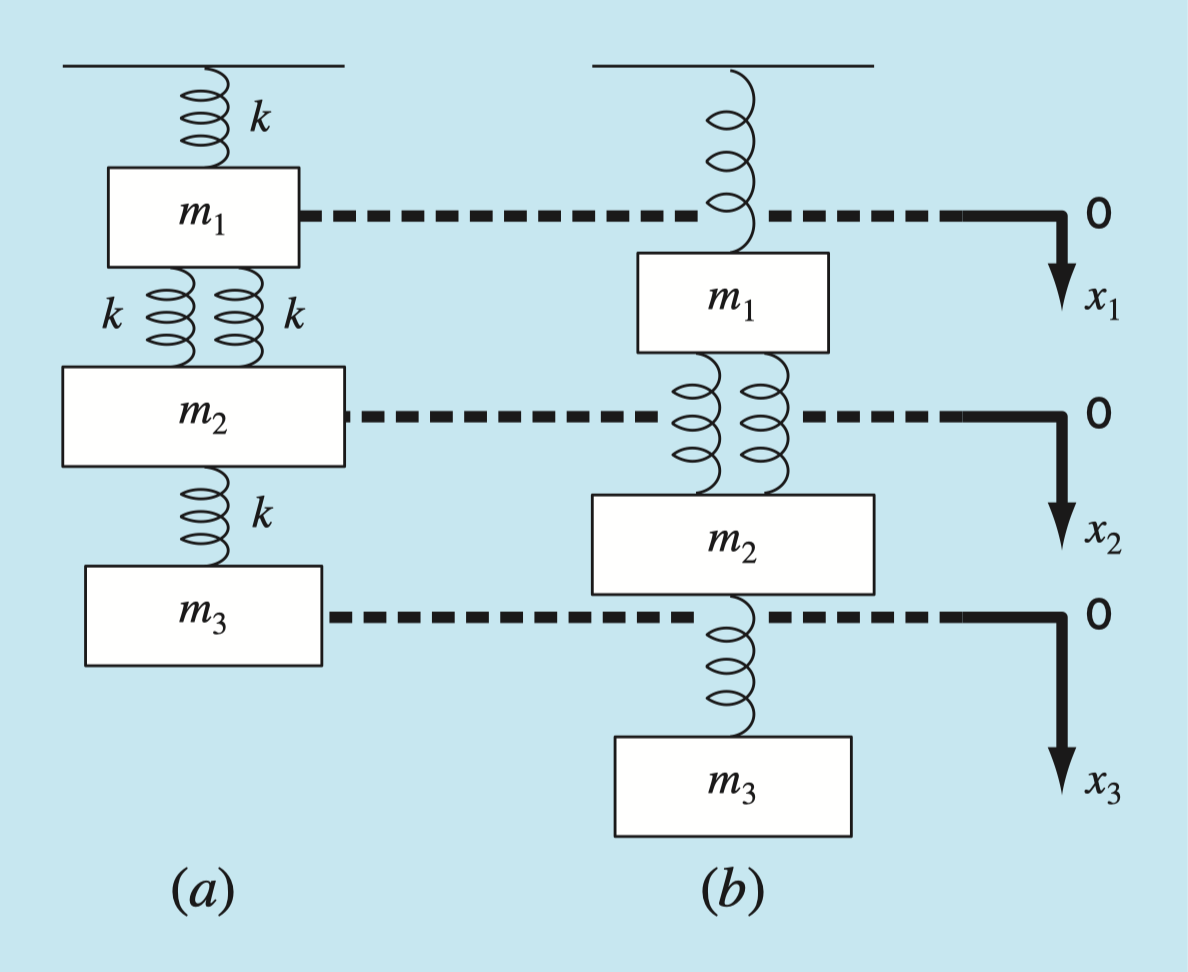
Given:

\(k = 10\) N/m
\(m_1 = 2\) kg, \(m_2=3\) kg, \(m_3 = 2.5\) kg

Find:

\(x_1\), \(x_2\), and \(x_3\)

Assume the system is at-rest.

Engineering example

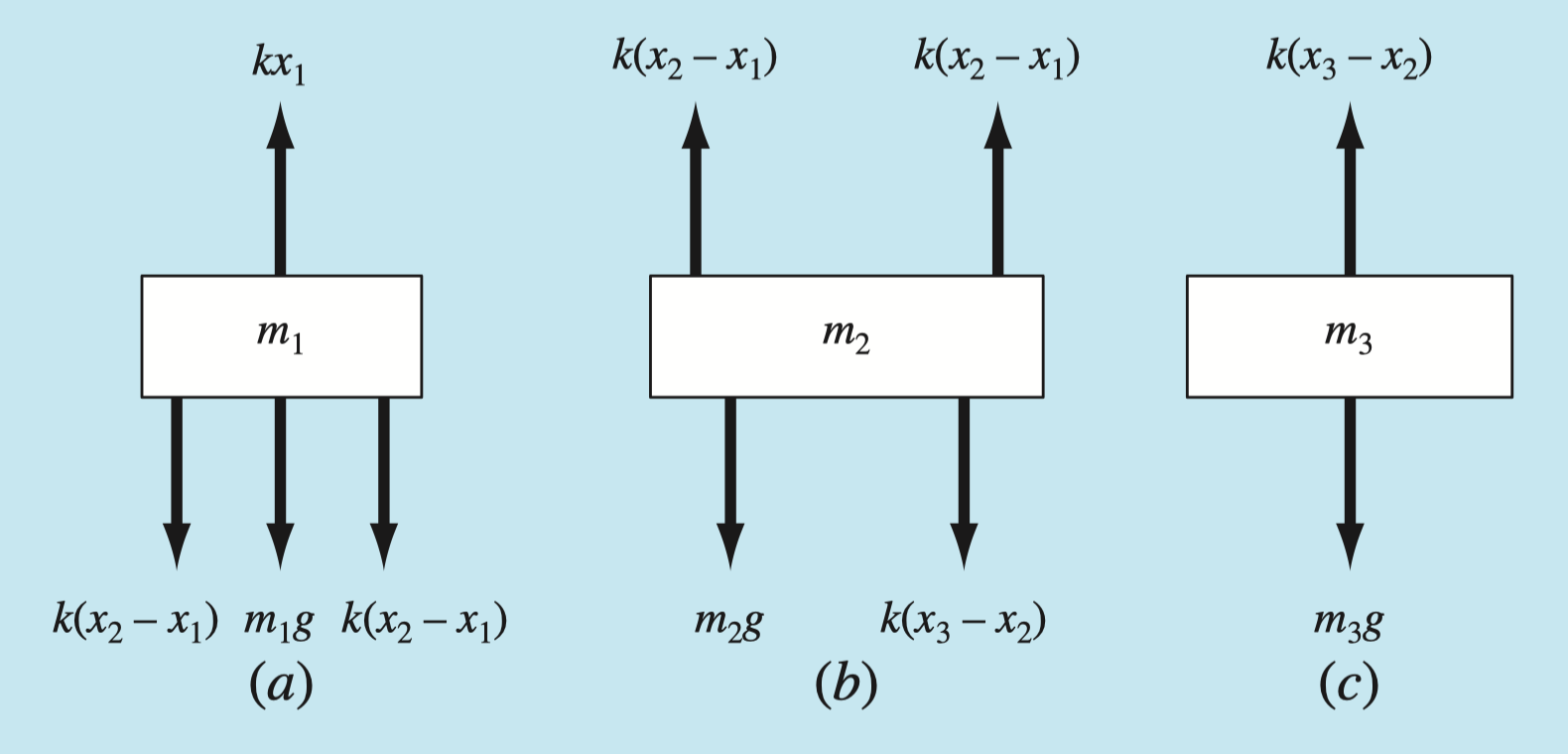
For each mass, \(\sum F = F_{up} - F_{down} = 0\)

Engineering example

Summing forces on each mass:

\[ \sum F = kx_1 - 2k(x_2 - x_1) - m_1 g = 0 \]

\[ \sum F = 2k(x_2 - x_1) - k(x_3 - x_2) - m_2 g = 0 \]

\[ \sum F = k(x_3 - x_2) - m_3 g = 0 \]

Engineering example

Let’s group items by the unknowns, \(x_1\), \(x_2\), and \(x_3\), and move the gravitational forces to the other side:

\[ \begin{matrix} 3kx_1 & - 2kx_2 & \ & = & m_1 g \\ -2kx_1 & + 2kx_2 &-kx_3& = & m_2 g \\ \ & - kx_2 &+ kx_3 &=& m_3g \end{matrix} \]

Engineering example

And then put the system of equations into the form \(A{\bf{x}} = \bf{b}\):

\[ \begin{matrix} 3kx_1 & - 2kx_2 & \ & = & m_1 g \\ -2kx_1 & + 2kx_2 &-kx_3& = & m_2 g \\ \ & - kx_2 &+ kx_3 &=& m_3g \end{matrix} \]

\[ A= \begin{bmatrix} 3k & -2k & 0\\ -2k & 2k & -k \\ 0 & -k & k \\ \end{bmatrix} \]

\[ {\bf{x}} \to \begin{bmatrix} x_1\\ x_2\\ x_3\\ \end{bmatrix} \]

\[ {\bf{b}} \to \begin{bmatrix} m_1g\\ m_2g\\ m_3g\\ \end{bmatrix} \]

Mass-spring example in Python

k = 10 # N/m
m1, m2, m3 = 2, 3, 2.5 # kg
g = 9.81 # m/s/s

A = k * np.array([
    [3, -2, 0],
    [-2, 3, -1],
    [0, -1, 1]])
b = [m1*g, m2*g, m3*g]
x = linalg.solve(A, b)
print(x)

[ 7.3575  10.05525 12.50775]

Making it “singlular”

k = 10 # N/m
m1, m2, m3 = 2, 3, 2.5 # kg
g = 9.81 # m/s/s

# alter A to remove any influence
# from the spring connecting m1 to
# the anchor point... no longer 
# a statics problem!
A = k * np.array([
    [0, -2, 0],
    [0, 3, -1],
    [0, -1, 1]])
b = [m1*g, m2*g, m3*g]
x = linalg.solve(A, b)
print(x)

---------------------------------------------------------------------------
LinAlgError                               Traceback (most recent call last)
Cell In[6], line 14
      9 A = k * np.array([
     10     [0, -2, 0],
     11     [0, 3, -1],
     12     [0, -1, 1]])
     13 b = [m1*g, m2*g, m3*g]
---> 14 x = linalg.solve(A, b)
     15 print(x)

File ~/GitHub/TME_310_students/.venv/lib/python3.11/site-packages/scipy/_lib/_util.py:1233, in _apply_over_batch.<locals>.decorator.<locals>.wrapper(*args, **kwargs)
   1231 # Early exit if call is not batched
   1232 if not any(batch_shapes):
-> 1233     return f(*arrays, *other_args, **kwargs)
   1235 # Determine broadcasted batch shape
   1236 batch_shape = np.broadcast_shapes(*batch_shapes)  # Gives OK error message

File ~/GitHub/TME_310_students/.venv/lib/python3.11/site-packages/scipy/linalg/_basic.py:272, in solve(a, b, lower, overwrite_a, overwrite_b, check_finite, assume_a, transposed)
    269 gecon, getrf, getrs = get_lapack_funcs(('gecon', 'getrf', 'getrs'),
    270                                        (a1, b1))
    271 lu, ipvt, info = getrf(a1, overwrite_a=overwrite_a)
--> 272 _solve_check(n, info)
    273 x, info = getrs(lu, ipvt, b1,
    274                 trans=trans, overwrite_b=overwrite_b)
    275 _solve_check(n, info)

File ~/GitHub/TME_310_students/.venv/lib/python3.11/site-packages/scipy/linalg/_basic.py:43, in _solve_check(n, info, lamch, rcond)
     41     raise ValueError(f'LAPACK reported an illegal value in {-info}-th argument.')
     42 elif 0 < info or rcond == 0:
---> 43     raise LinAlgError('Matrix is singular.')
     45 if lamch is None:
     46     return

LinAlgError: Matrix is singular.