Numerical differentiation
TME 310 - Computational Physical Modeling
University of Washington Tacoma
Numerical differentiation
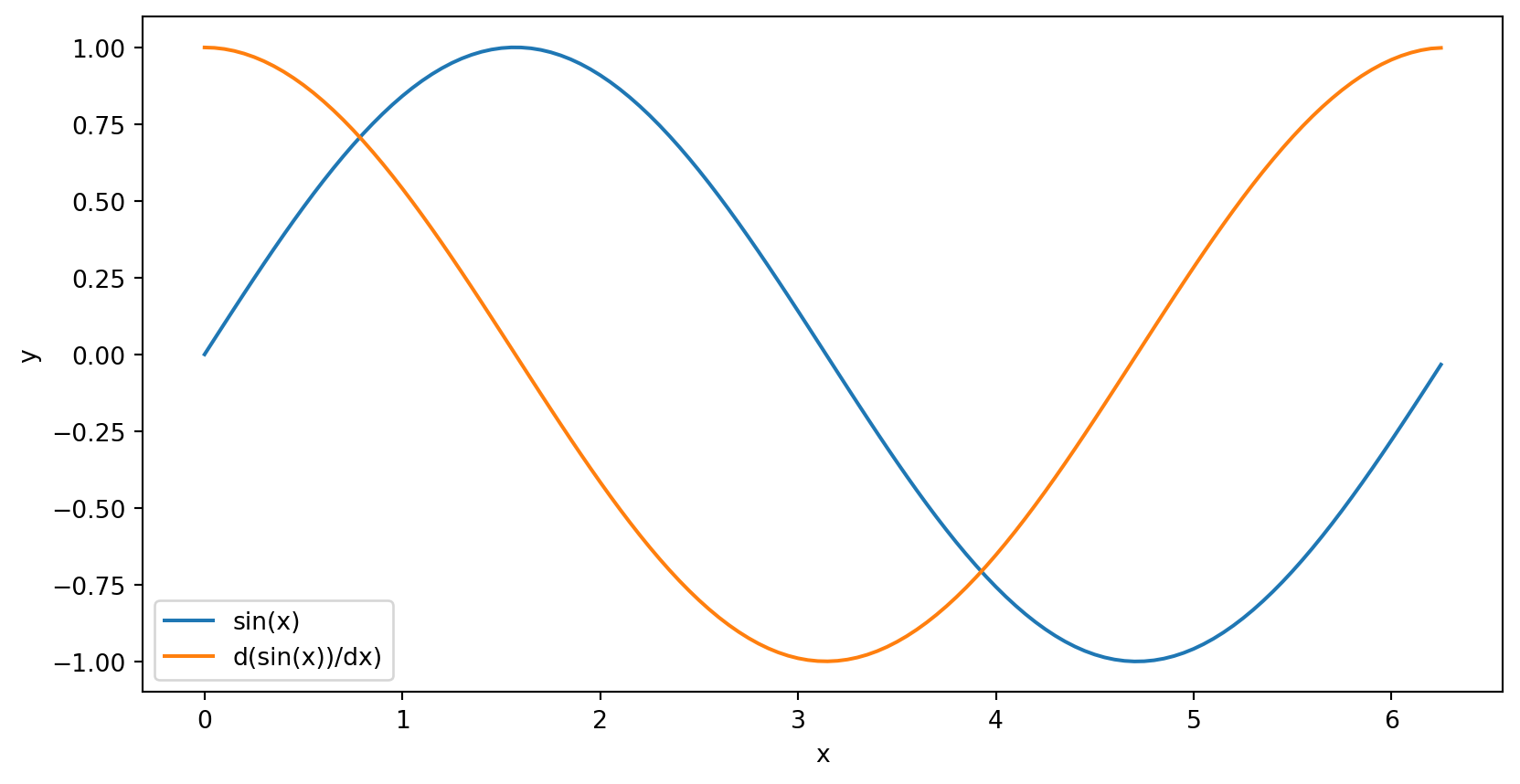
What is a derivative?
A function or value that describes
- The “rate” of change of a function
- The slope of a function
- \(\displaystyle f'(x) = \frac{df(x)}{dx} = \frac{dy}{dx}\)
In calculus, we learned how to find derivatives analytically.
In this course, we’ll approximate derivatives numerically
Basic numerical derivatives
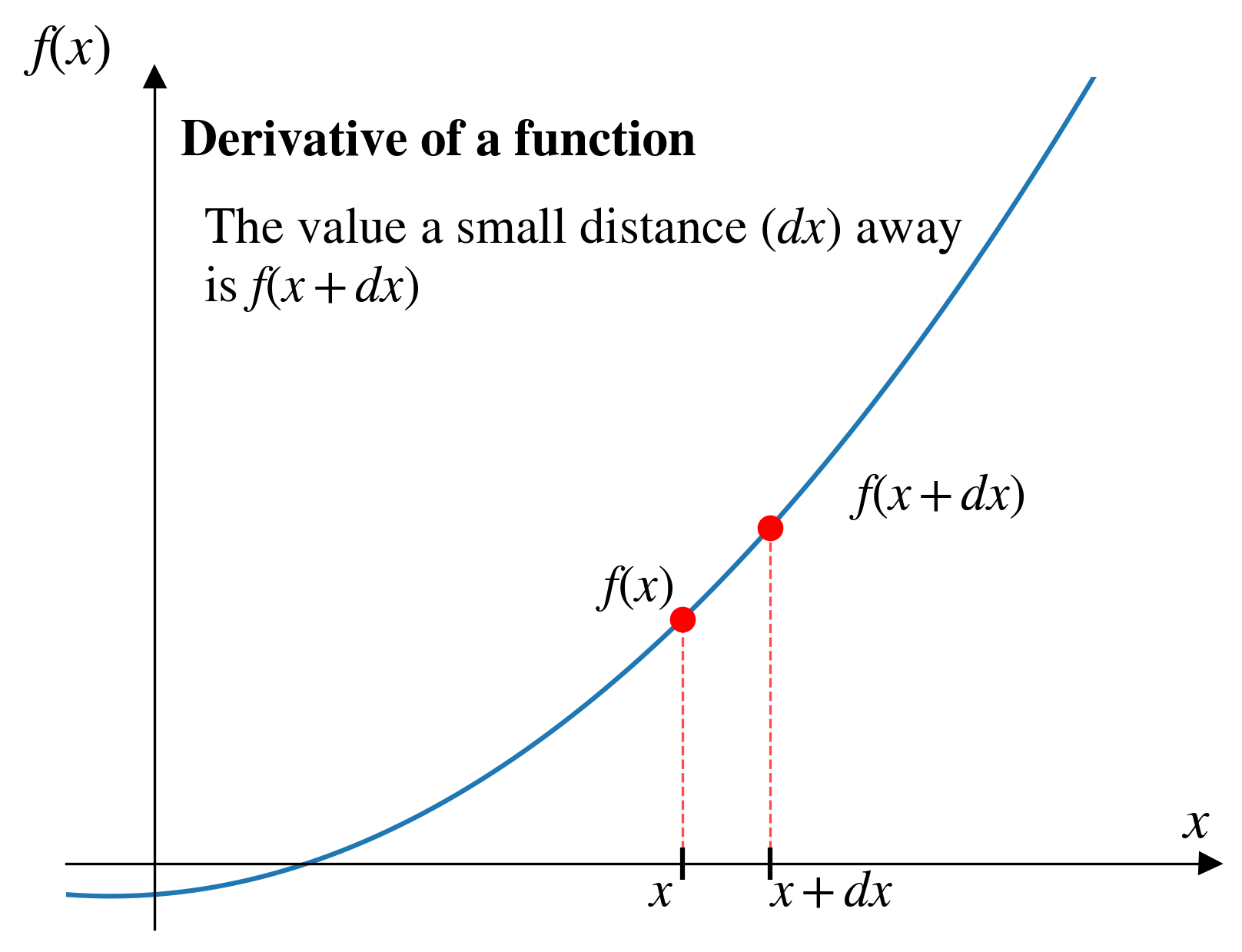
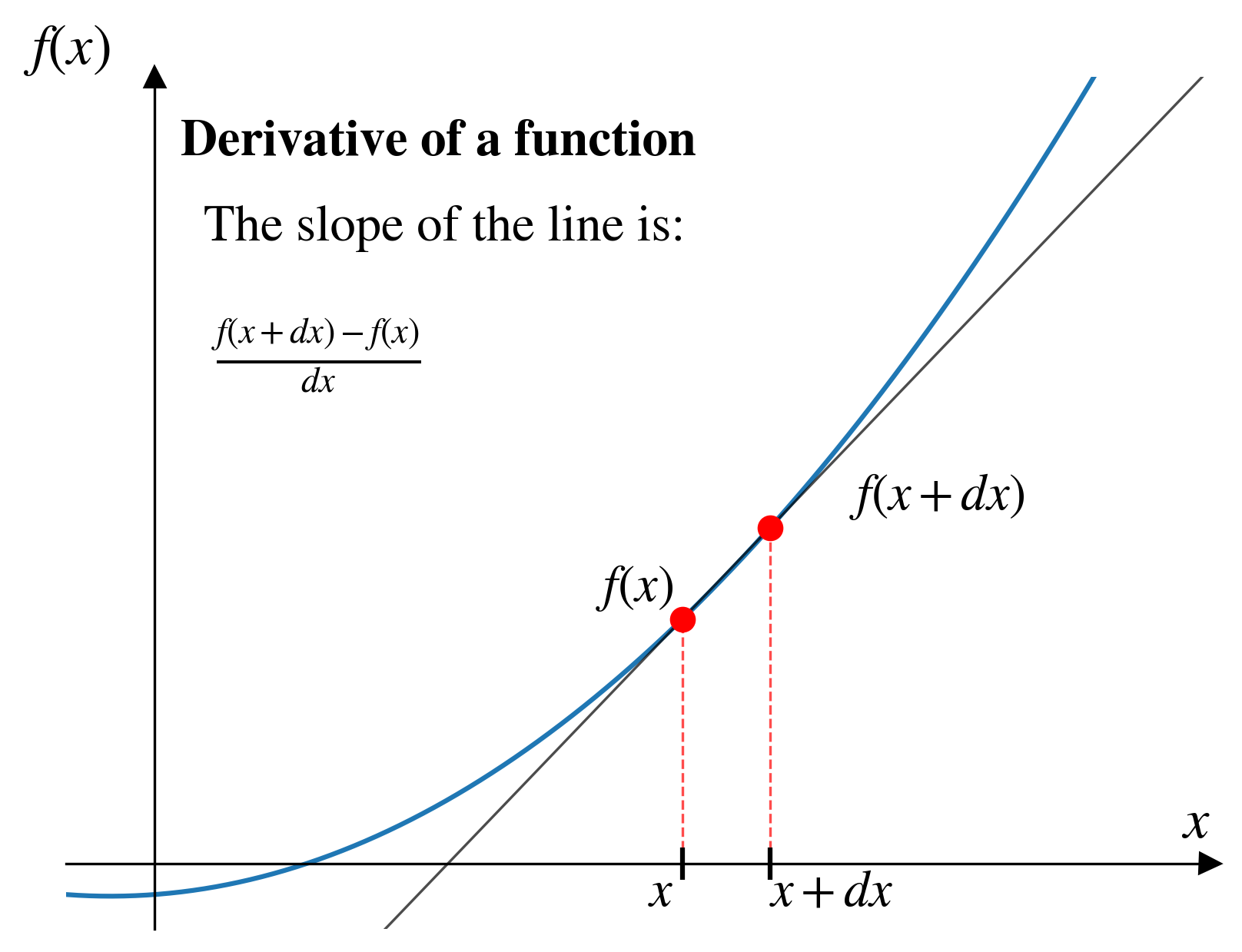
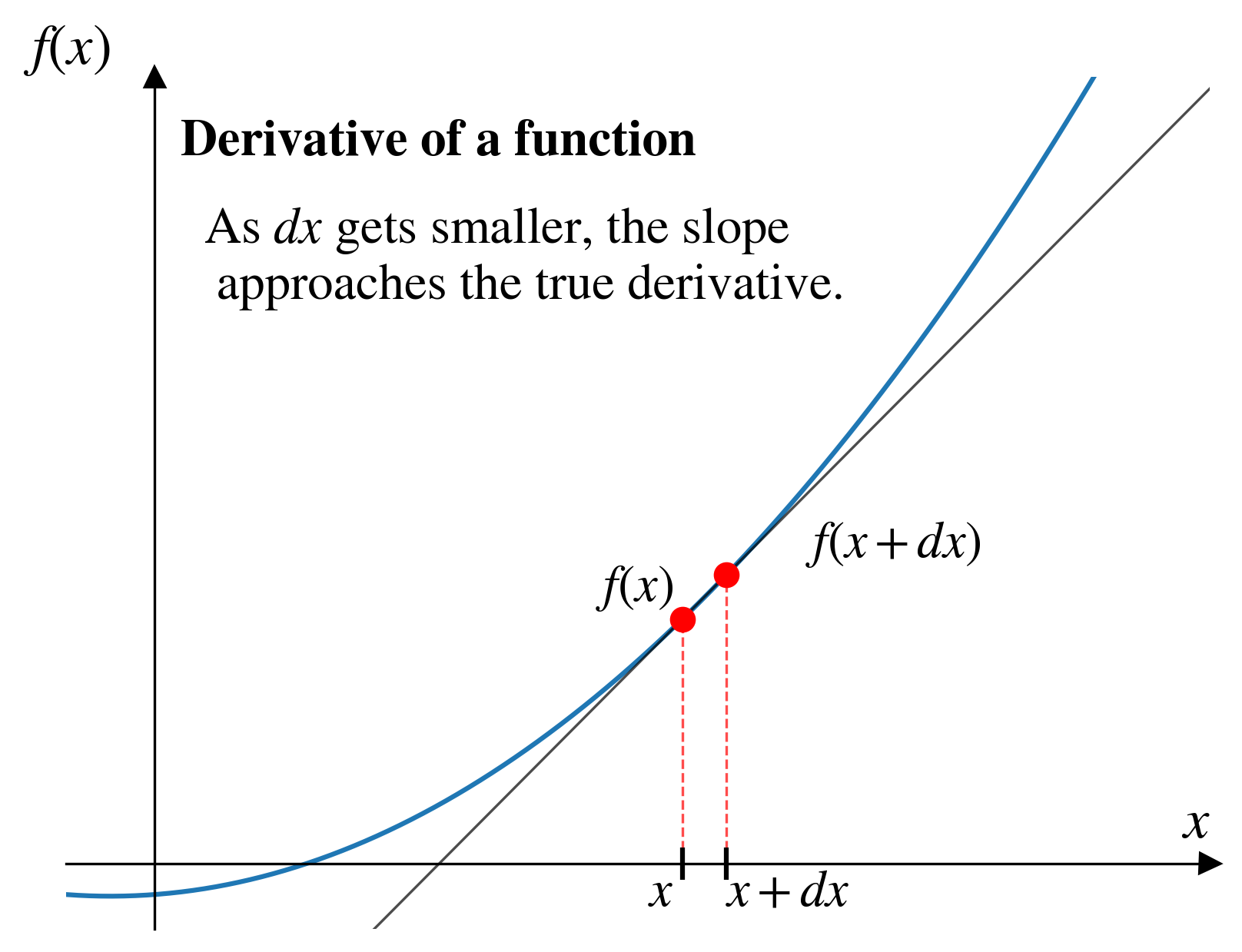
The definition of a derivative:
\[f'(x) = \lim_{dx \to 0} \frac{f(x + dx) - f(x)}{dx}\]
Basic numerical derivatives
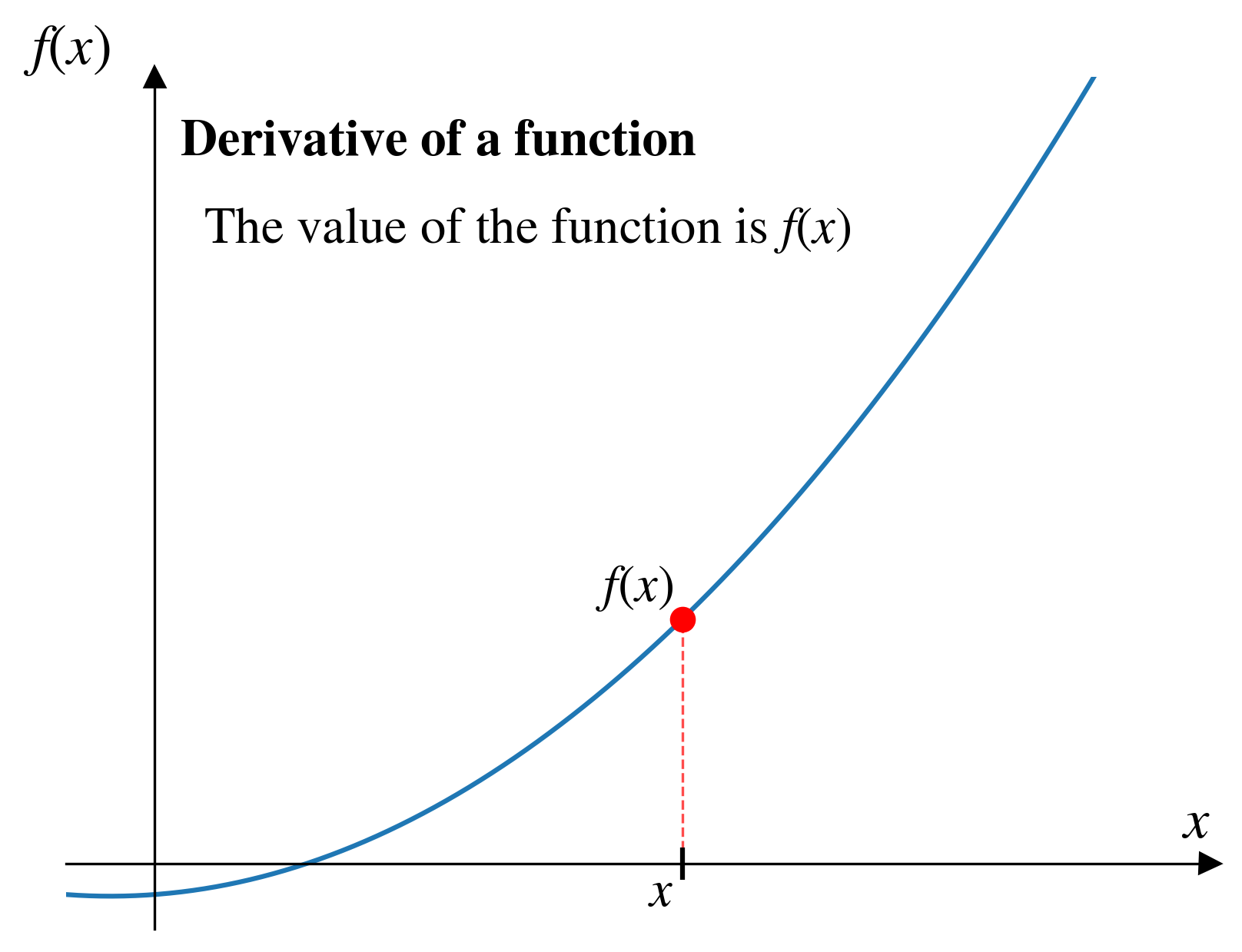
Discritizing functions
If we evaluate a function at intervals spaced at \(dx\), we are essentially converting our continuous function into a set of discrete data points.
From smooth to discrete
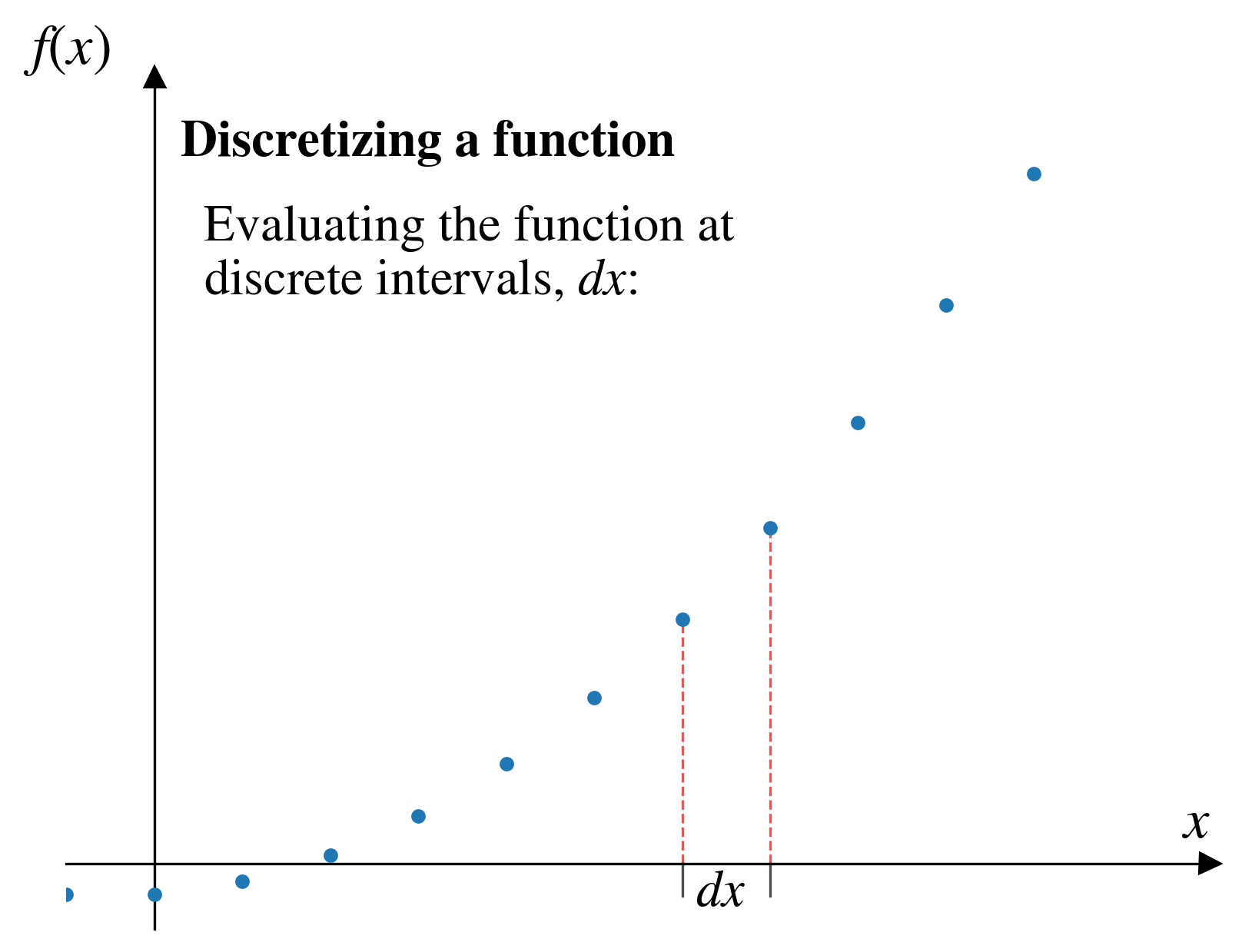
An example
We discretize functions every time we plot them
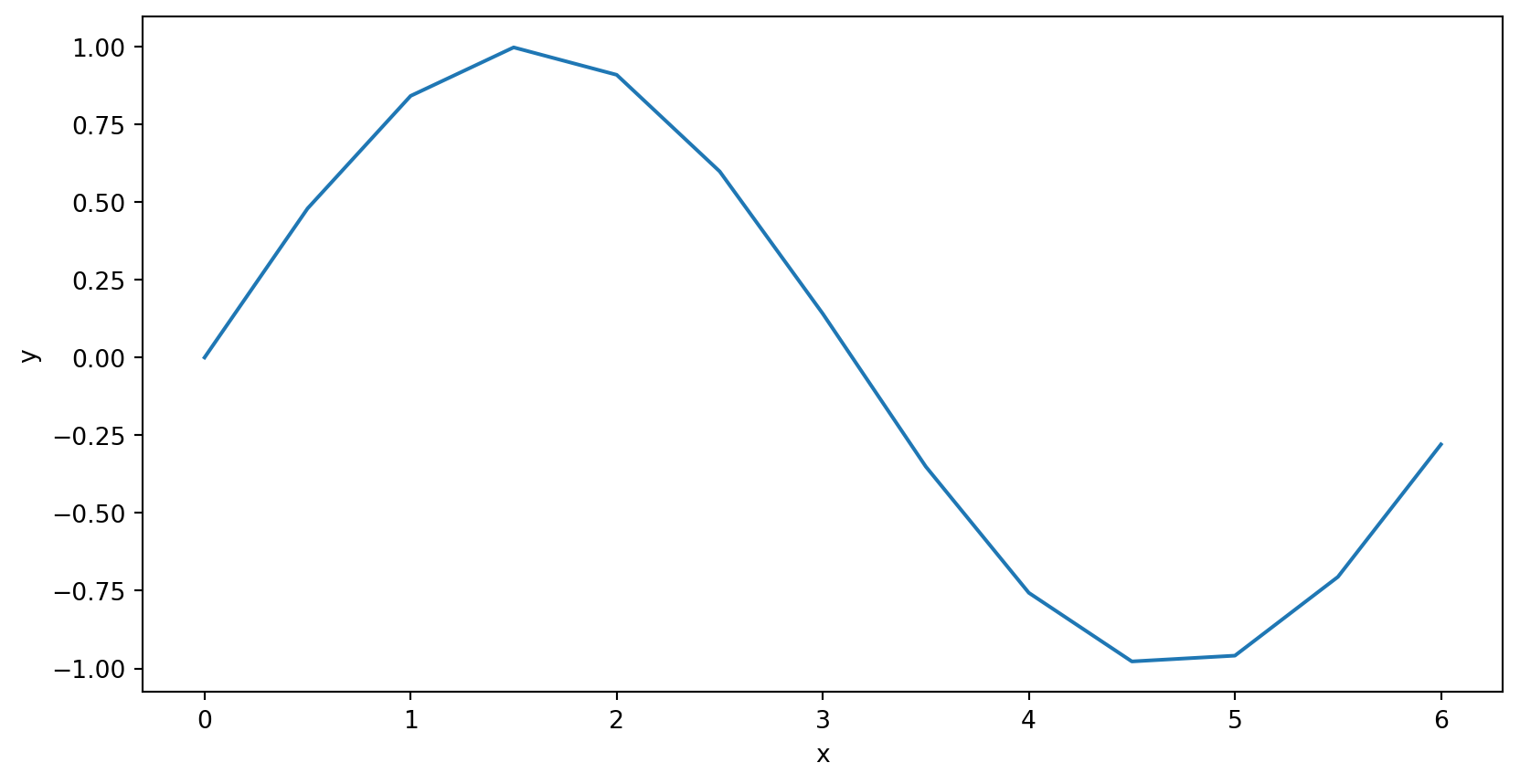
An example
We discretize functions every time we plot them
Numerical derivatives
Let’s apply these concepts to finding numerical derivatives using three simple approaches:
- Forward finite difference (FFD)
- Central finite difference (CFD)
- Backward finite difference (BFD)
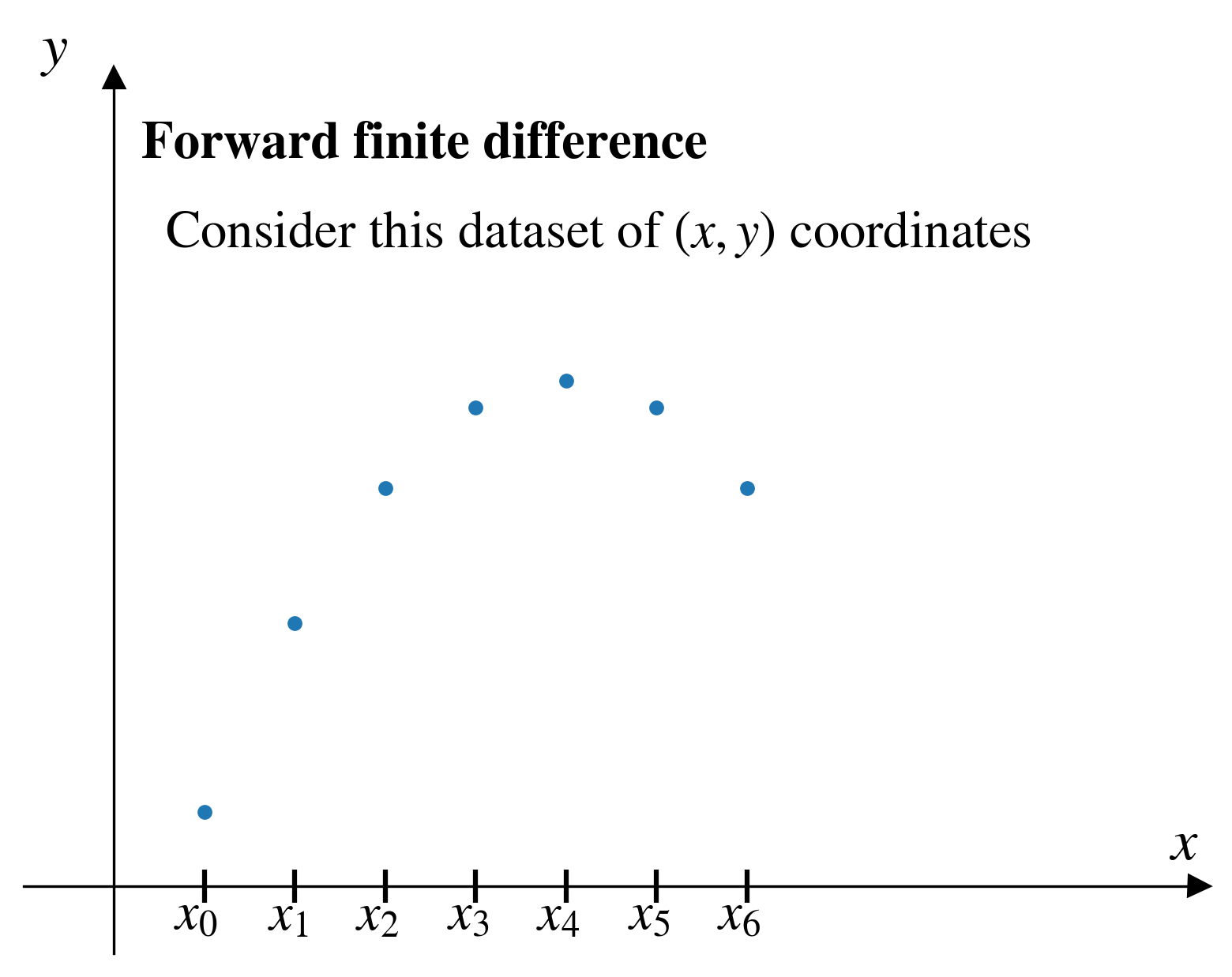
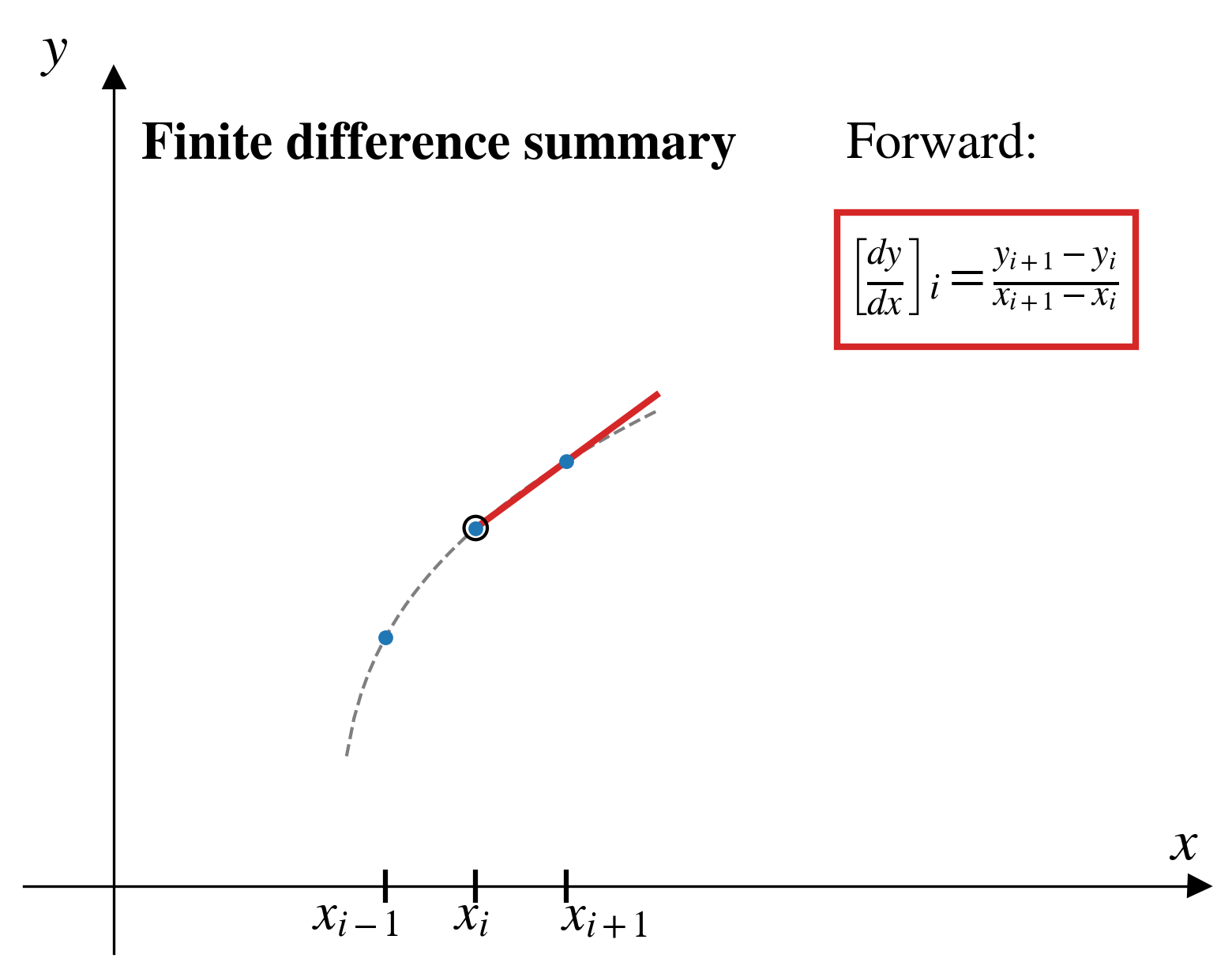
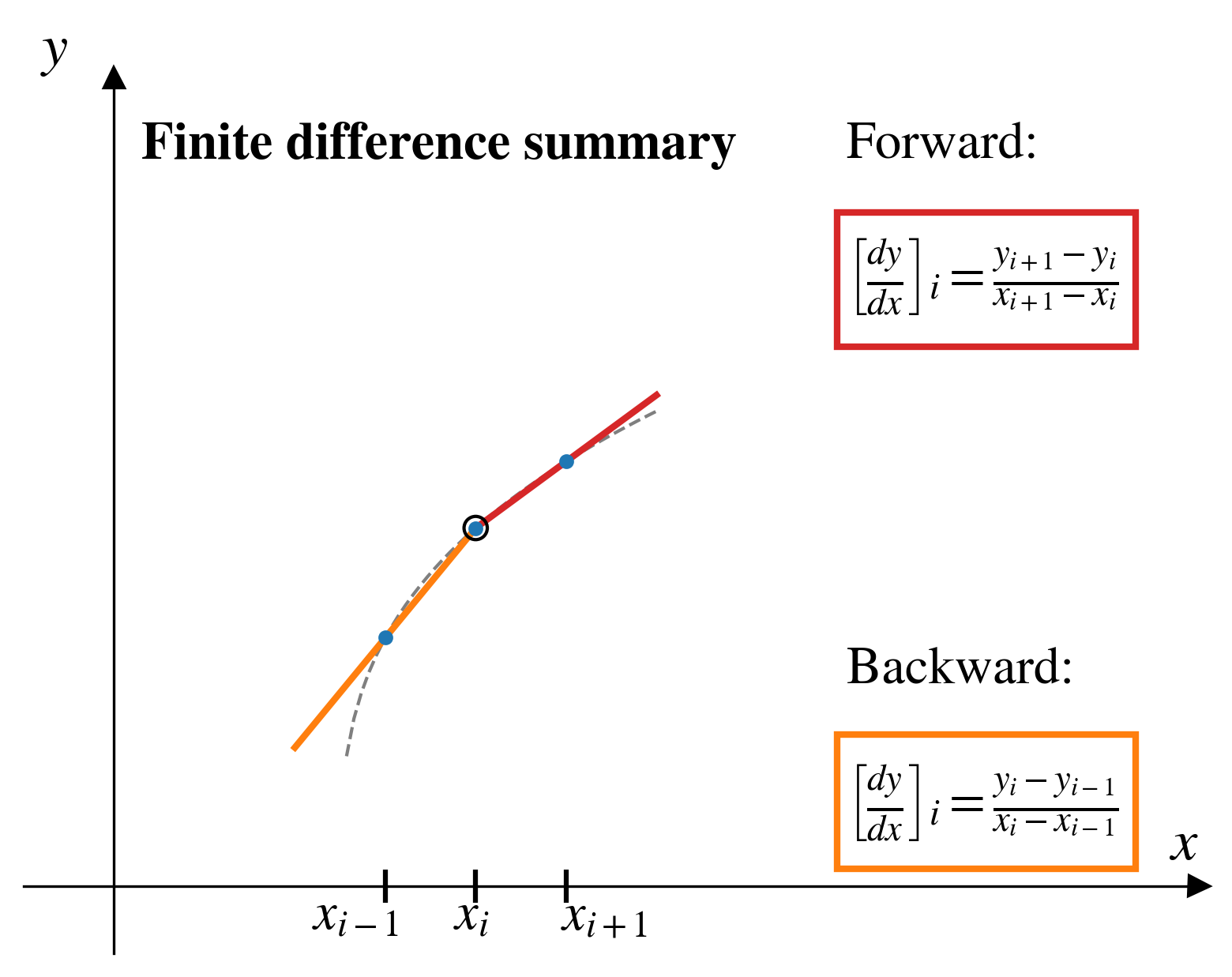
Forward finite difference
In the forward finite difference (FFD) method, from a given pair of points, \((x_i,y_i)\), we approximate the derivative by looking “forward” to the next pair of points, \((x_{i+1},y_{i+1})\)
\[ \left[\frac{dy}{dx}\right]_i = \frac{y_{i+1} - y_i}{x_{i+1} - x_i}\]
FFD

\((t_0, x_0, y_0)\)
\((t_1, x_1, y_1)\)
\((t_2, x_2, y_2)\)
\((t_n, x_n, y_n)\)
FFD

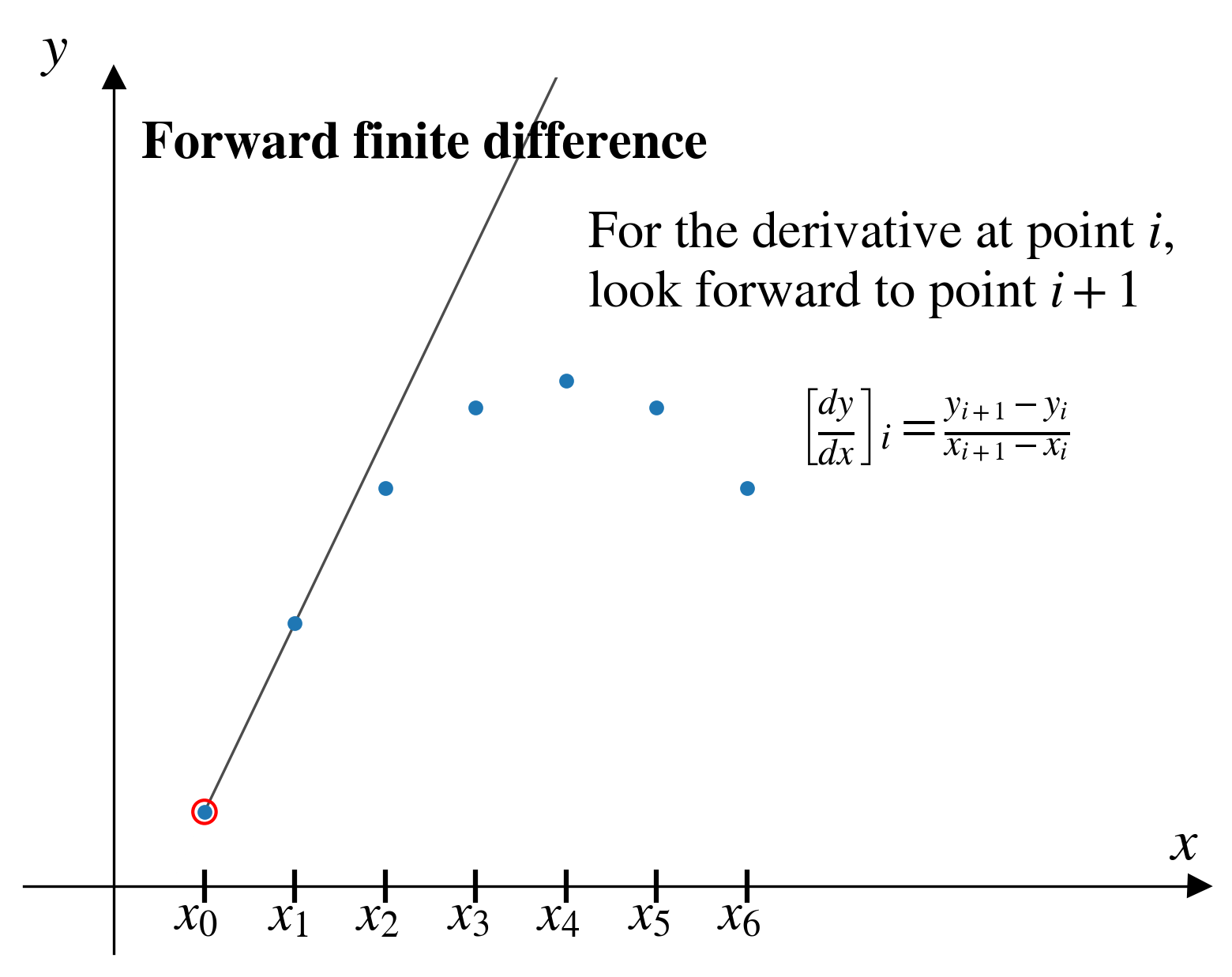
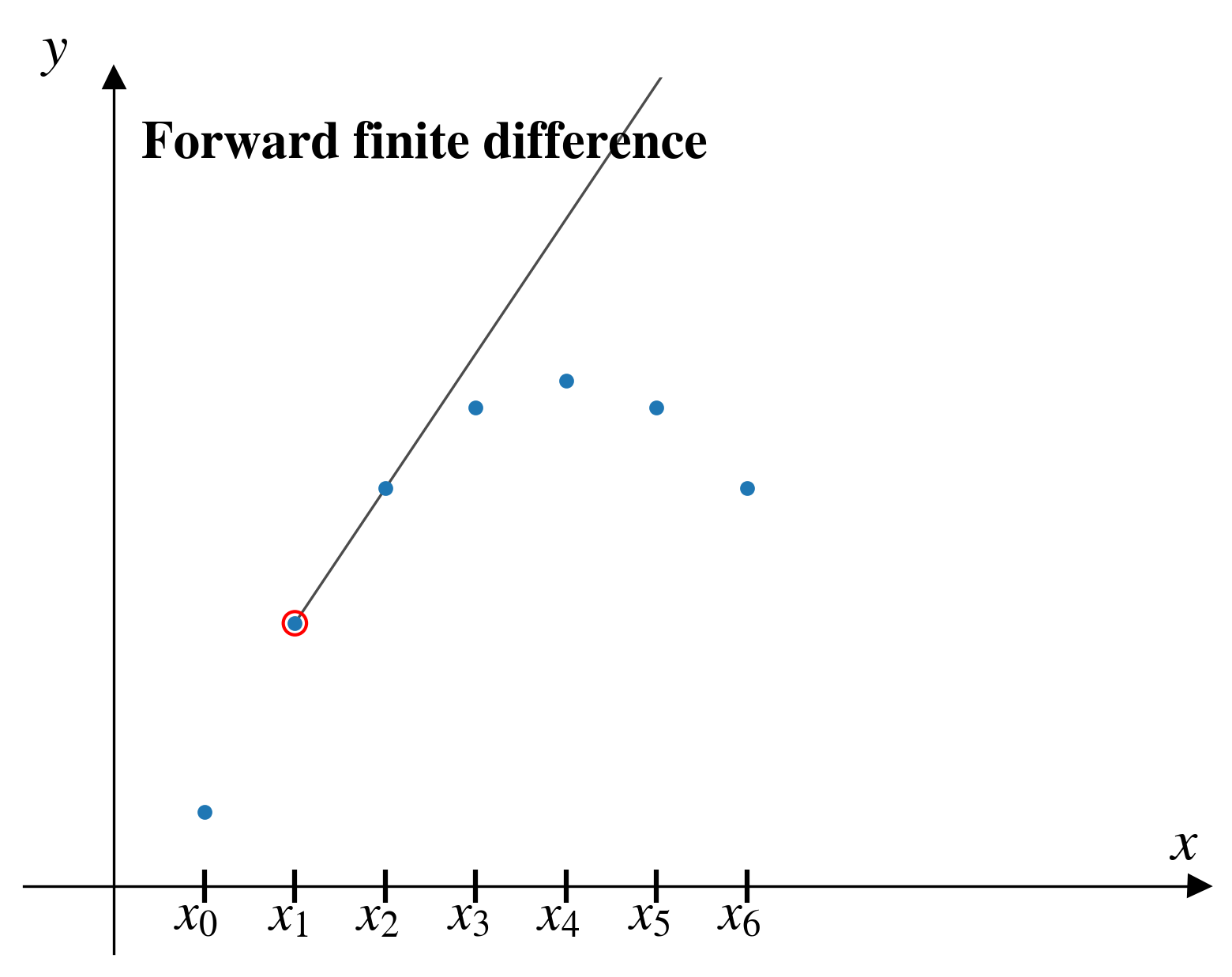
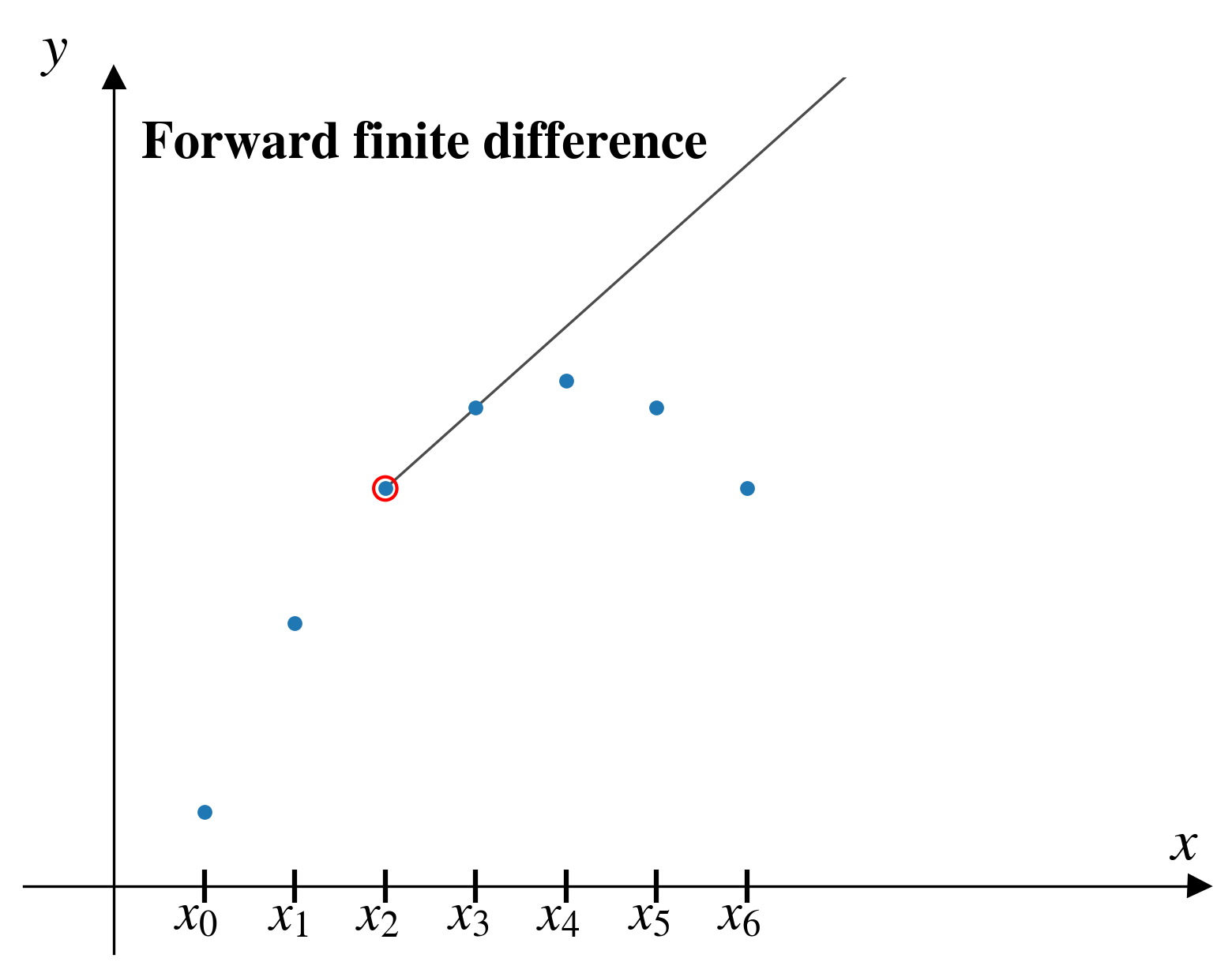
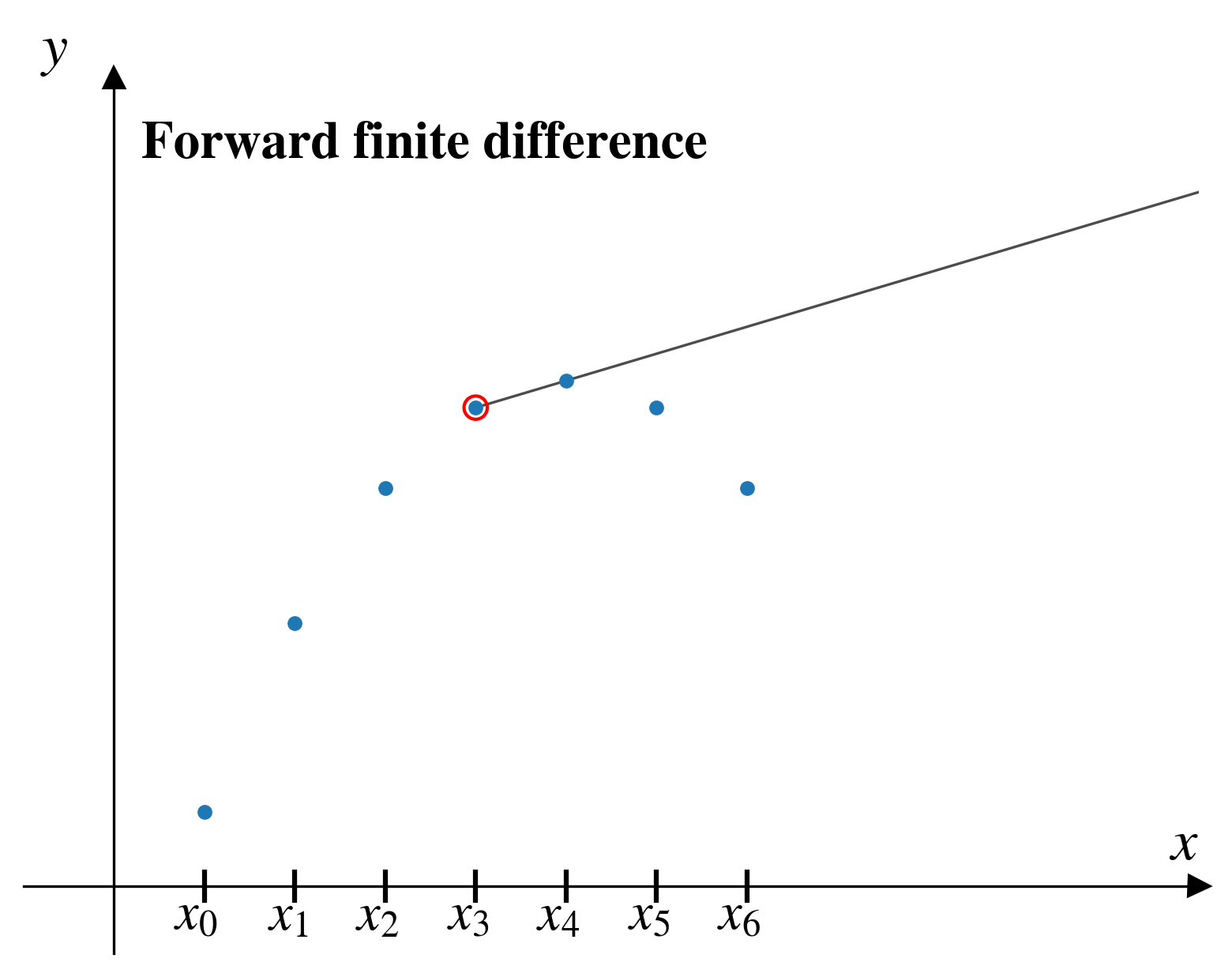
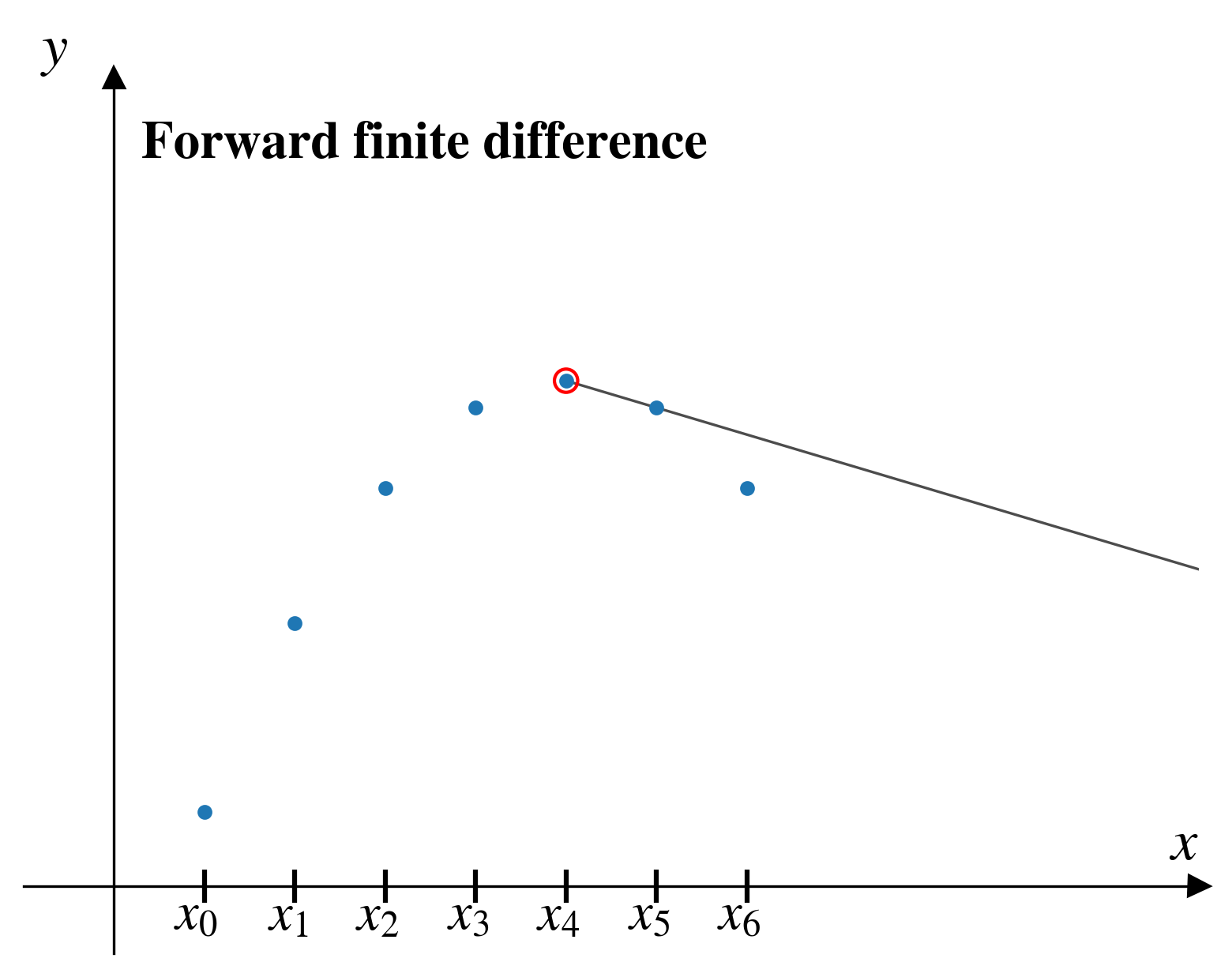
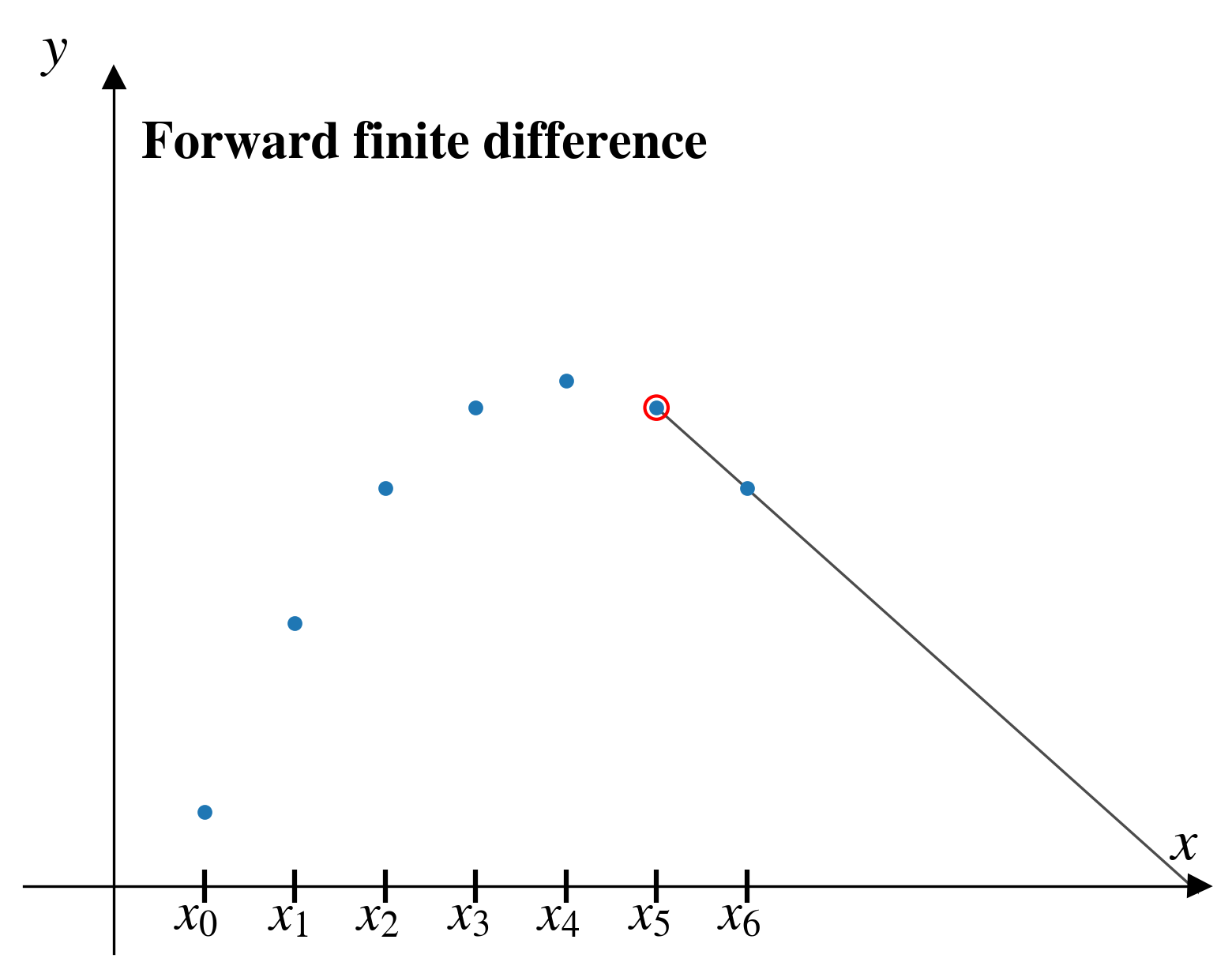
FFD problems
As we step through the FFD, two problems are apparent:
- We can’t estimate the derivative for our last data point!
For a dataset with \(n\) points, FFD will give us \(n-1\) estimates of the derivative.
- The estimate seems inaccurate in several places.
Let’s address issue 2 first
Central finite difference
In the central finite difference (CFD) method, from a given pair of points, \((x_i,y_i)\), we approximate the derivative by looking at the two pairs of points on either side: \((x_{i-1},y_{i-1})\) and \((x_{i+1},y_{i+1})\)
\[ \left[\frac{dy}{dx}\right]_i = \frac{y_{i+1} - y_{i-1}}{x_{i+1} - x_{i-1}}\]
CFD
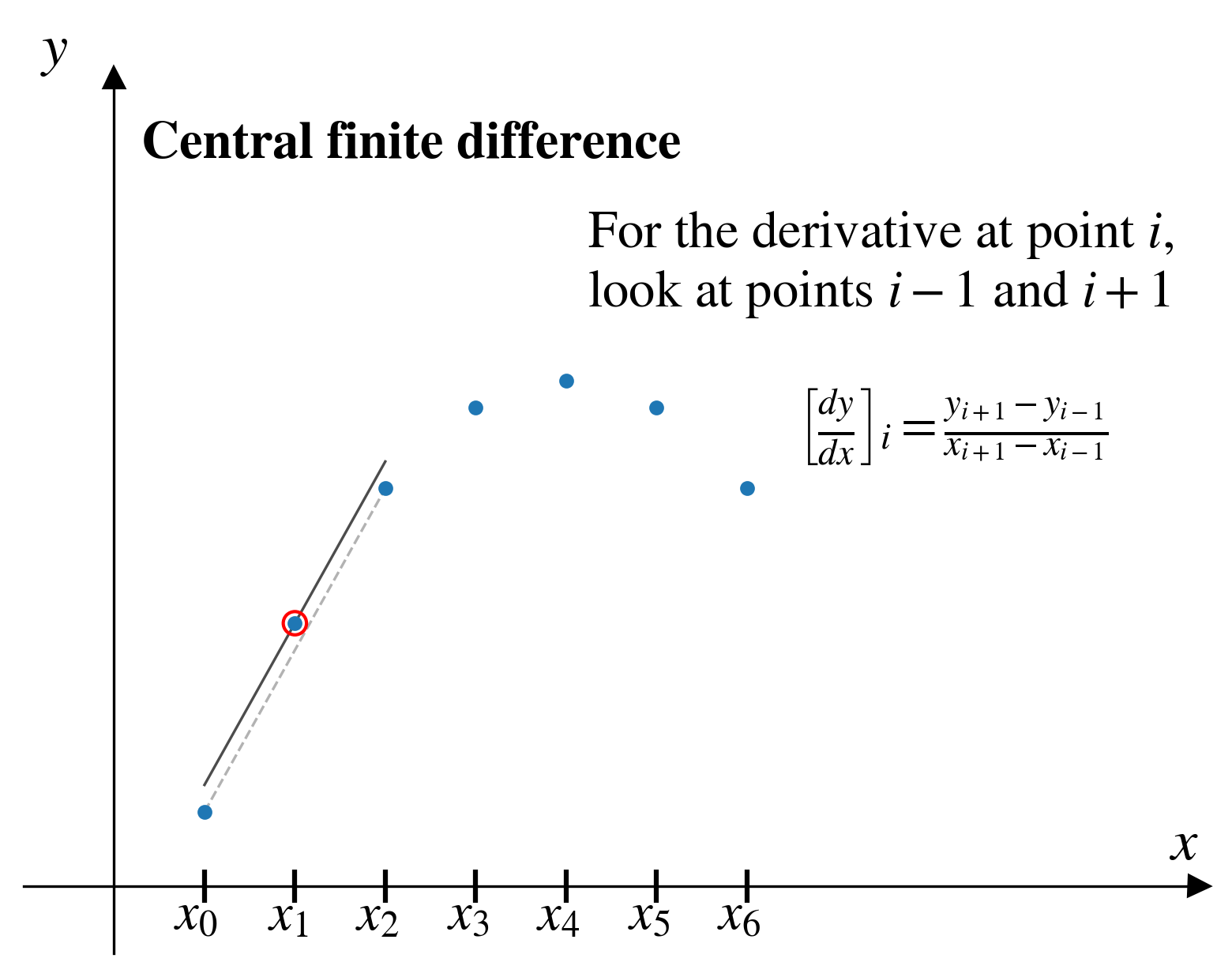
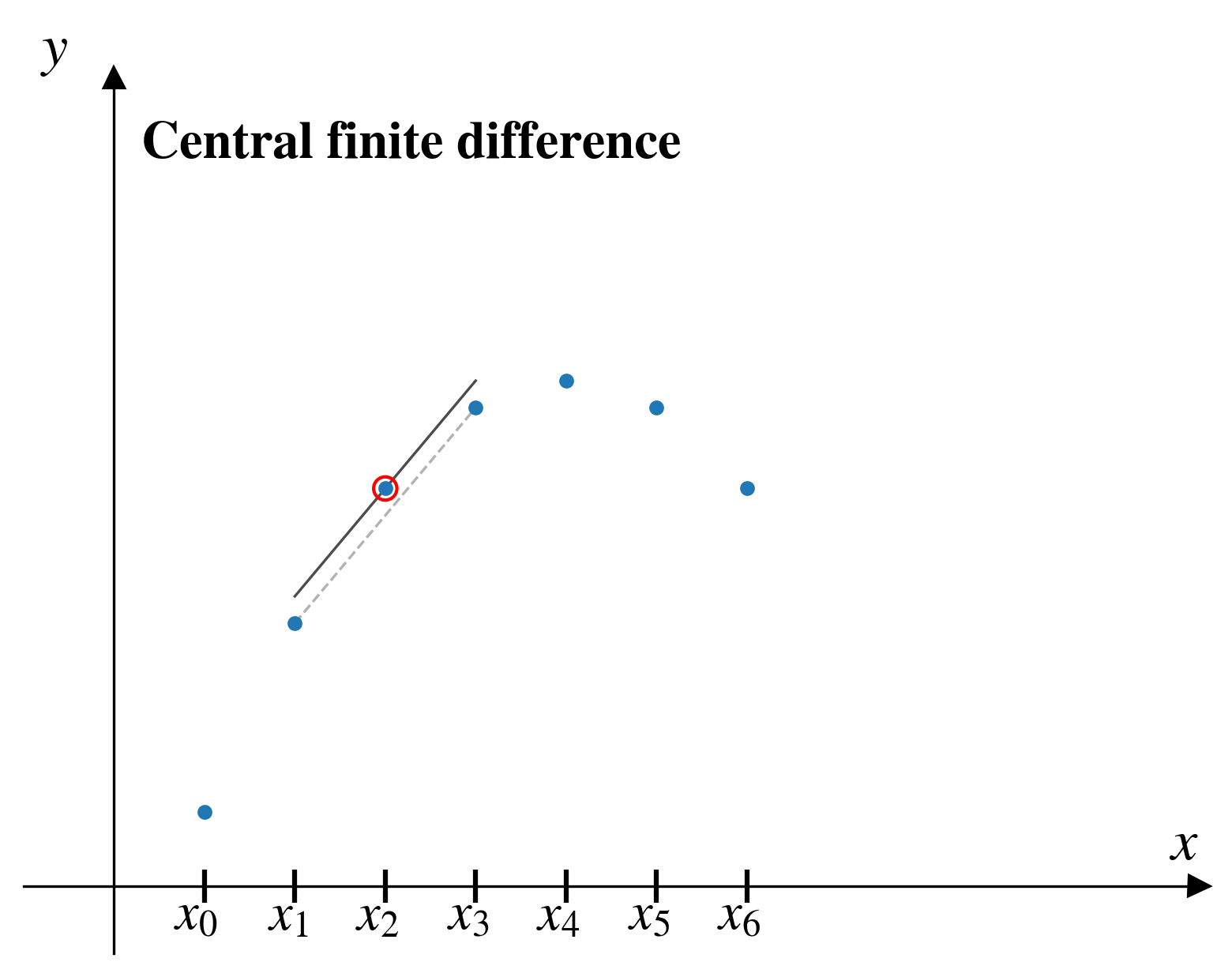
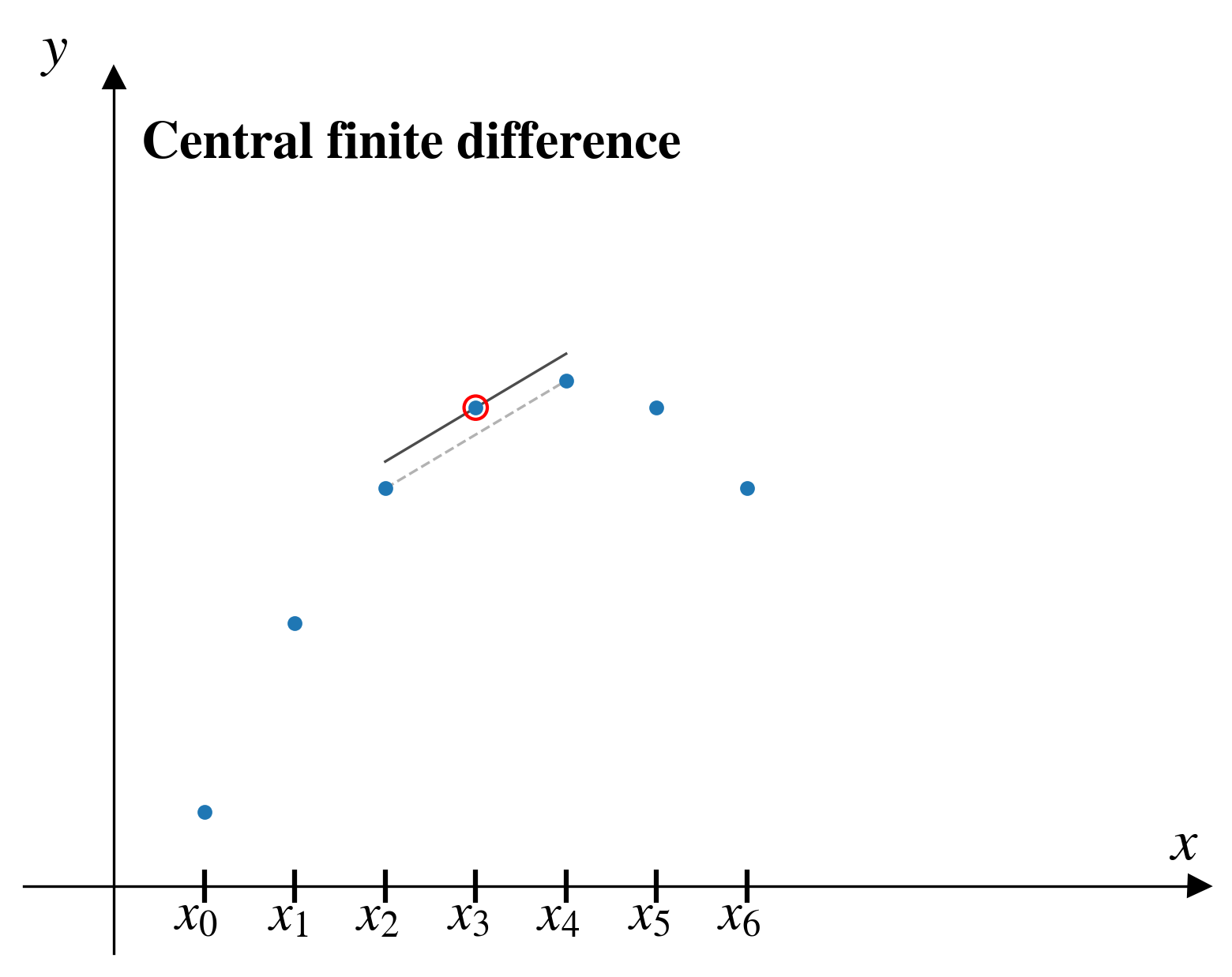
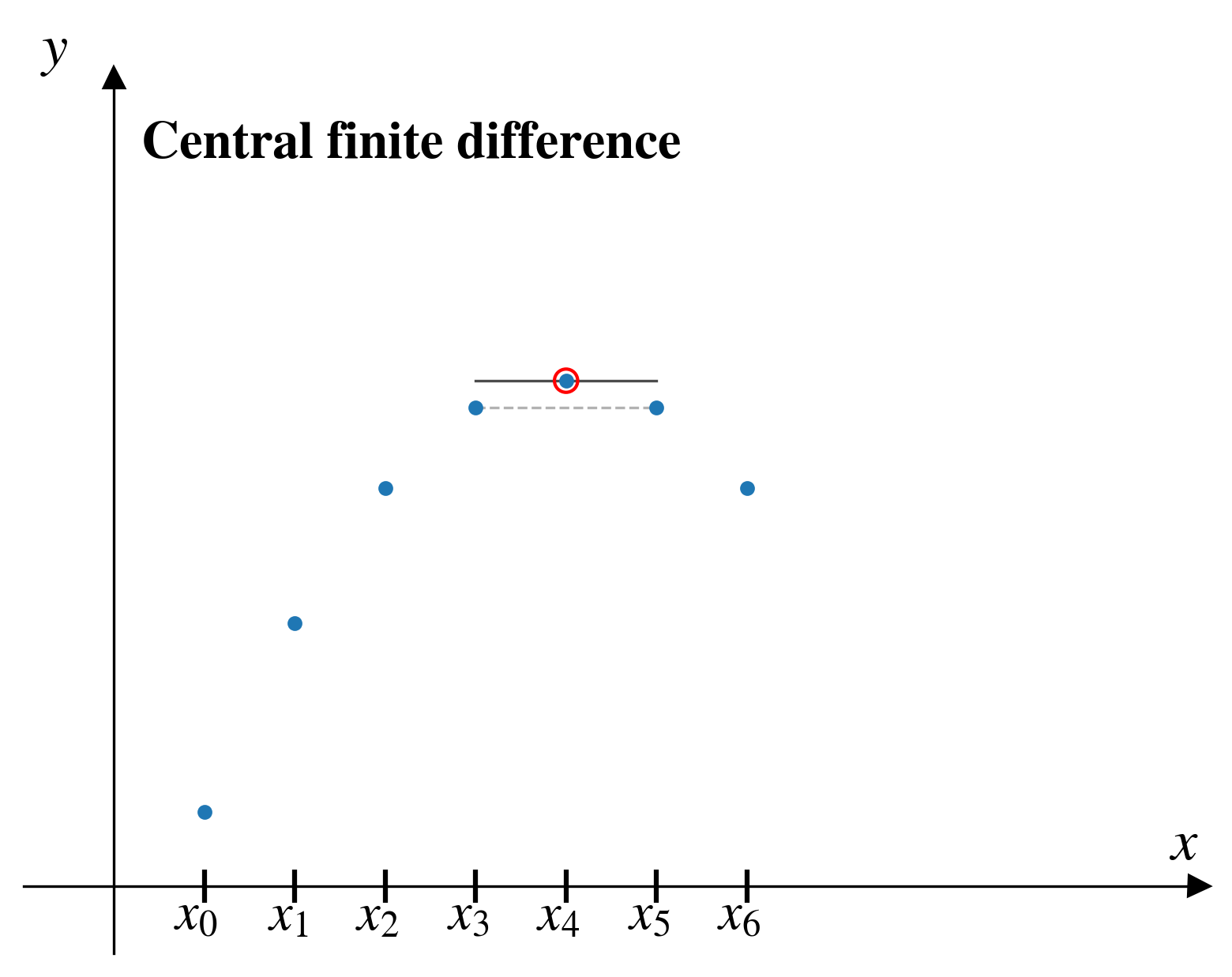
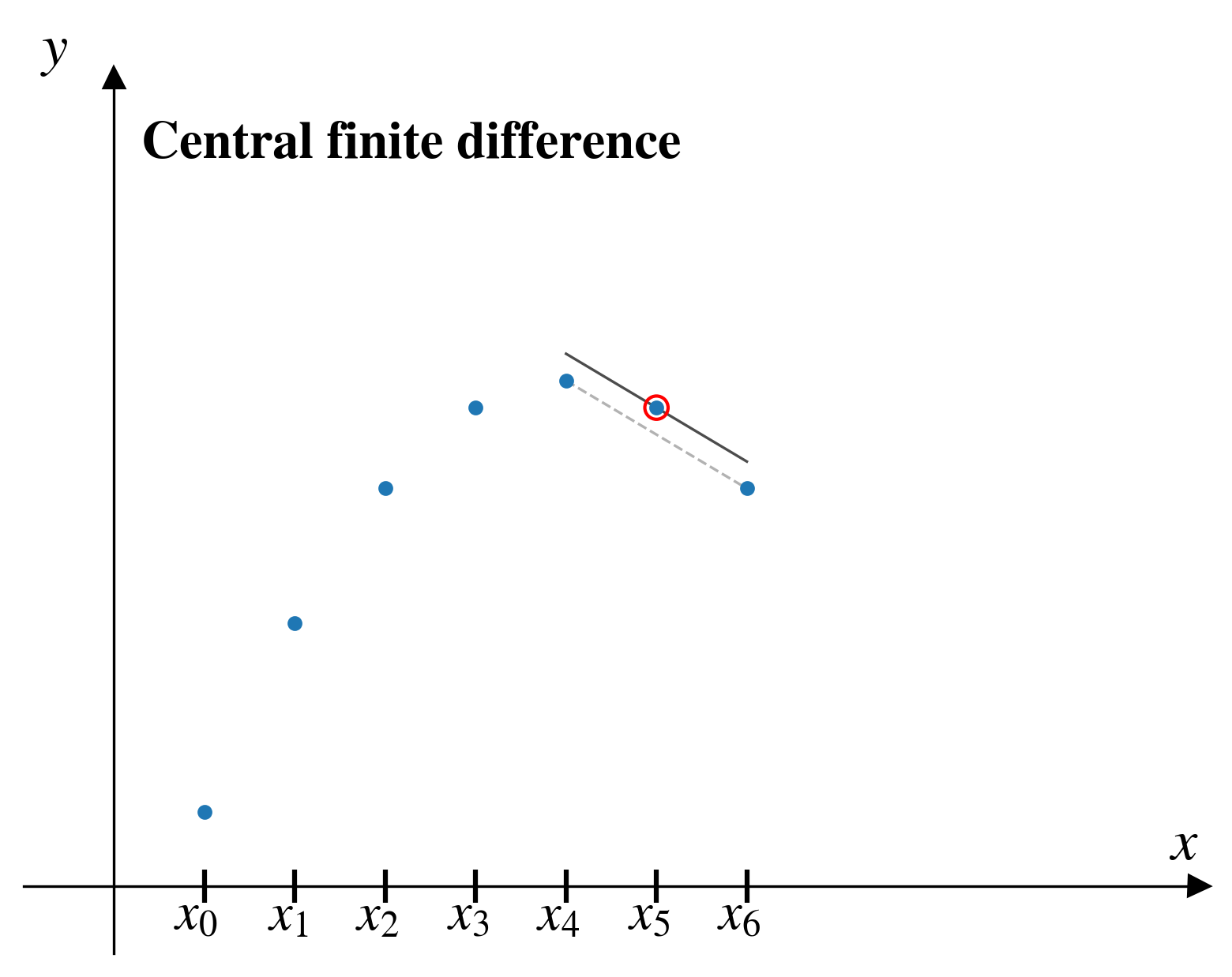
A partial improvement…
The central finite difference seems to
- improve the accuracy of the derivative estimate
- consider effect of data on both sides of the point of interest
But it has an even more limited range than the forward finite difference method:
For a dataset with \(n\) points, CFD will give us \(n-2\) estimates of the derivative.
Solution: use CFD wherever possible, use FFD when needed
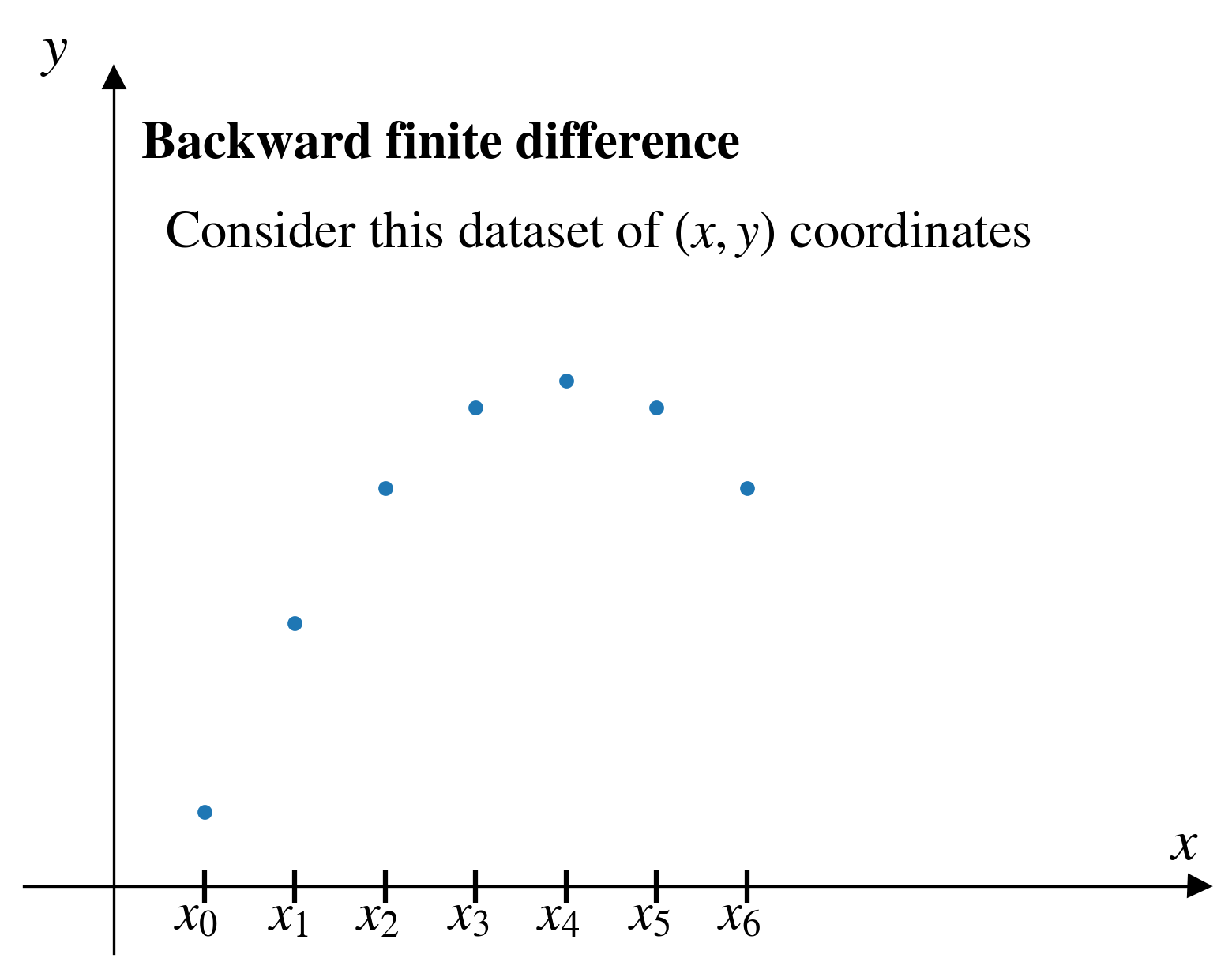
Backward finite difference
That still leaves us with \(n-1\) estimates…
Enter the backward finite difference method
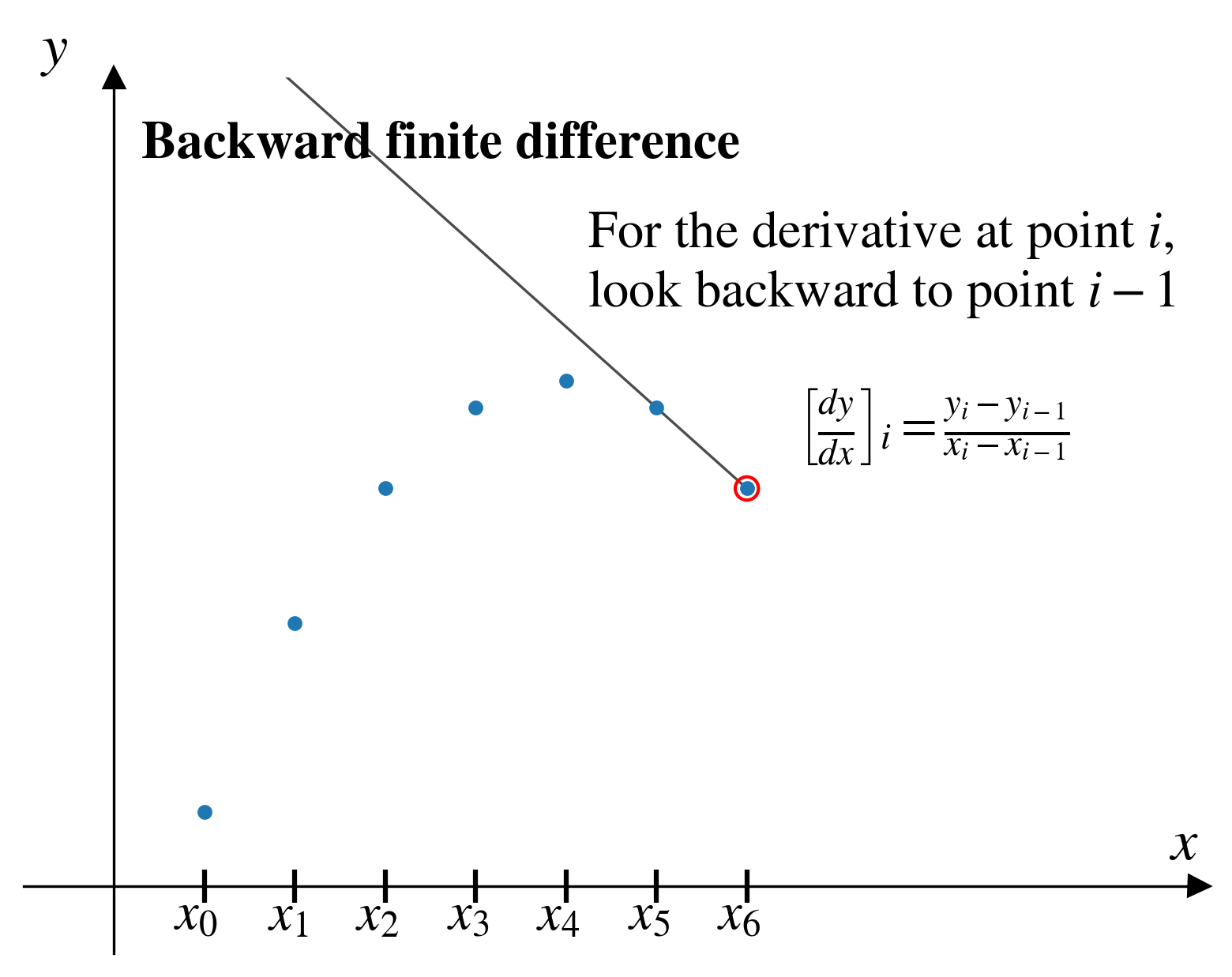
In the backward finite difference (BFD) method, from a given pair of points, \((x_i,y_i)\), we approximate the derivative by looking “backward” at the previous pair of points, \((x_{i-1},y_{i-1})\)
\[ \left[\frac{dy}{dx}\right]_i = \frac{y_{i} - y_{i-1}}{x_{i} - x_{i-1}}\]
BFD
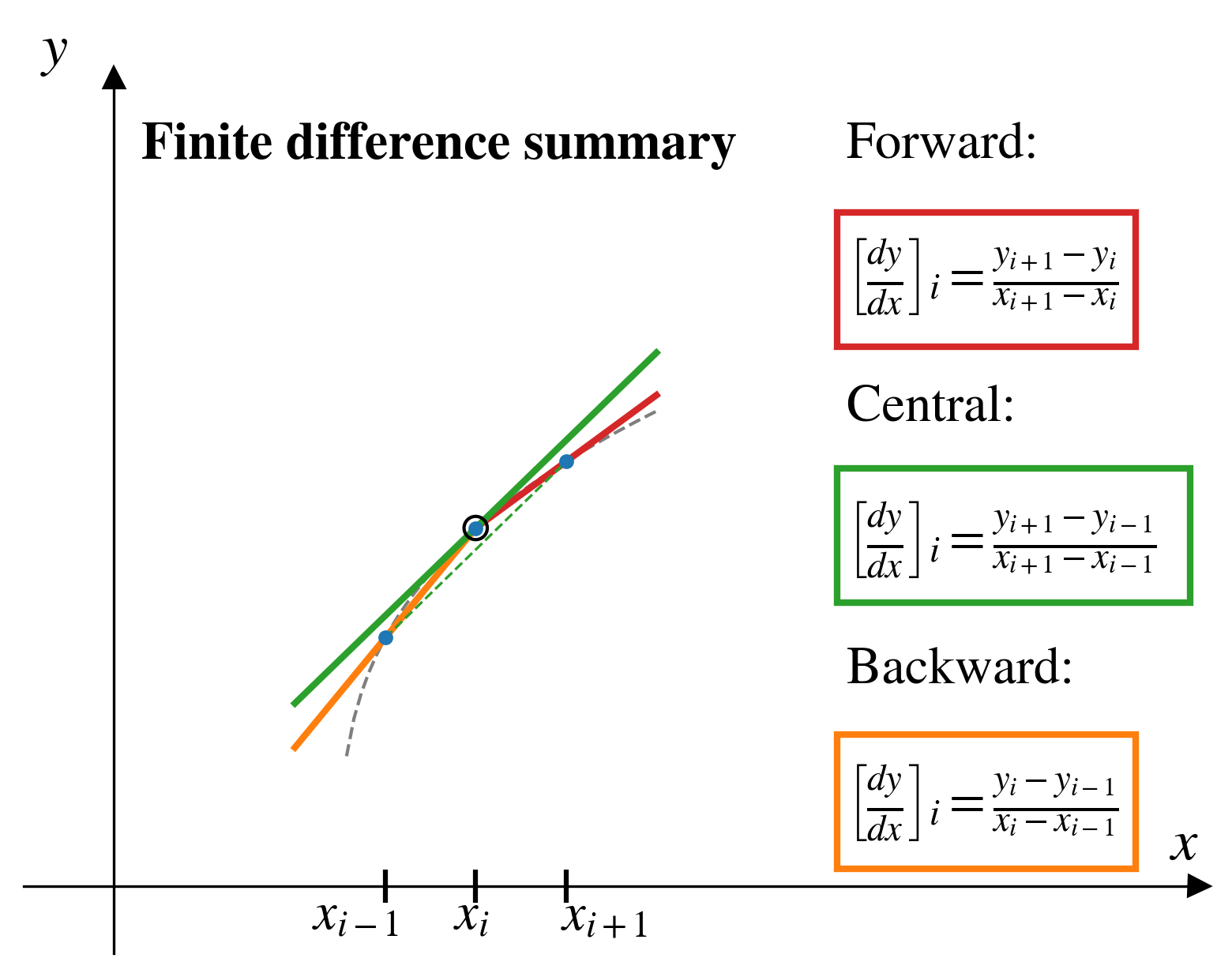
Where to use each method
Because it has the least error, the central finite difference method should be used wherever possible.
- Use the forward finite difference method to estimate the derivative of the first point.
- Use the backward finite difference method to estimate the derivative of the last point.
- Use the central finite difference method everywhere else.
Finite different methods summary
Differentiating with Numpy
Numpy has a function for discrete differentiation: numpy.gradient