n t y dy/dt TME 310 - Computational Physical Modeling
Euler’s Method for ODEs
University of Washington Tacoma
What is a differential equation?
Differential equation
an equation that relates an unknown function to its own derivative.
For example
\[y(t) = 3t + \frac{dy}{dt}\]
Analytical solutions
We’ve seen analytical solutions to differential equations.
For example, in the parachute problem, we used the solution to this differential equation: \[\frac{dv}{dt} = g -\frac{c}{m}v\]
which was:
\[ v(t) = \frac{gm}{c}(1 - e^{-ct/m})\]
Numerical solutions
But many differential equations don’t have closed-form (i.e., analytical) solutions.
For those, we need numerical methods to approximate solutions.
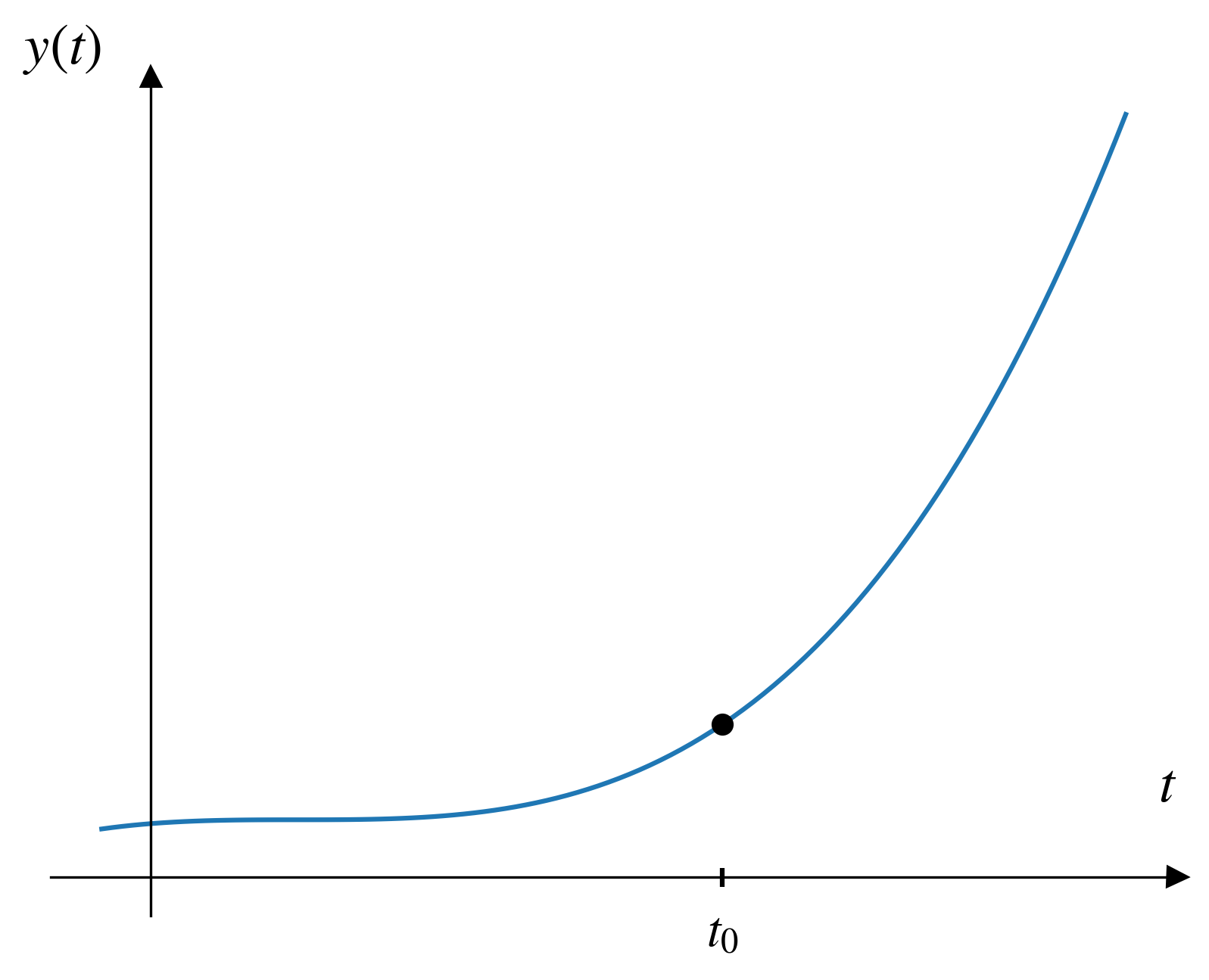
Euler’s Method

(1760’s) Euler developed a method that approximates the solution to a differential equation.
He realized that if
- I know the form of the differential equation (\(dy/dt = f(y,t)\))
- I know the value at one point (initial condition)
Then..
- I can estimate the value at some other time, very close to the known point.
- And I can keep doing that to get as many points as I want.
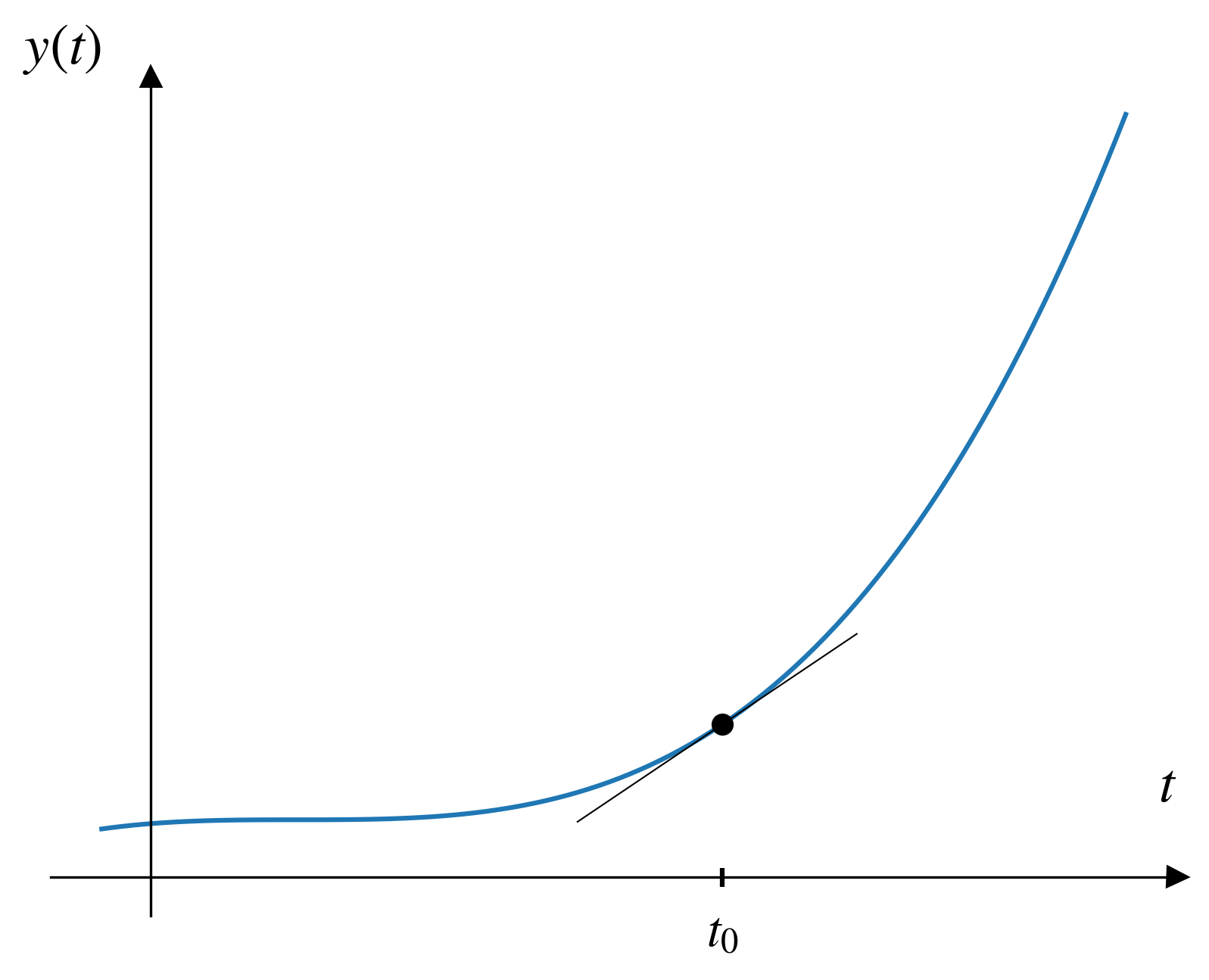
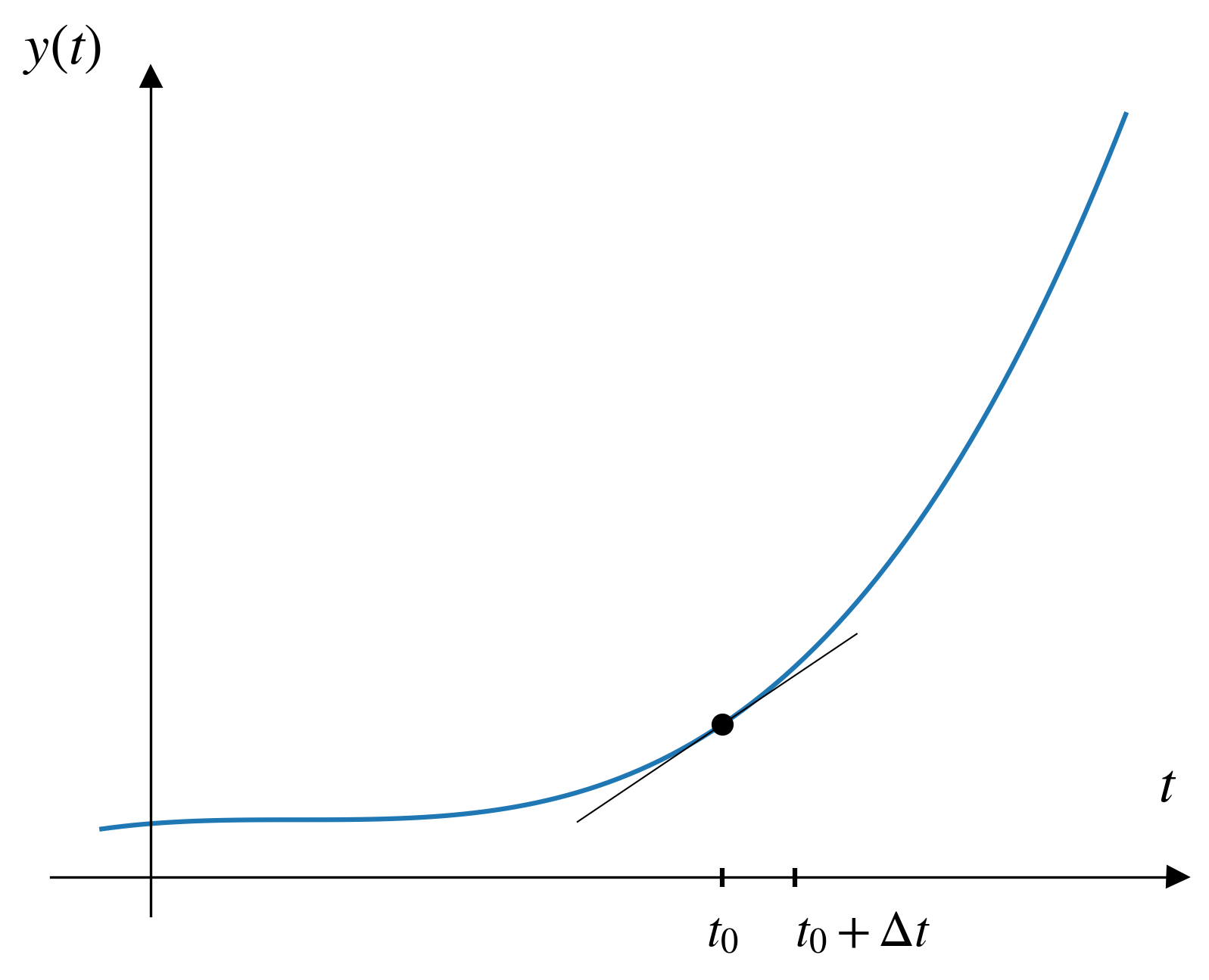
Visualizing Euler’s method
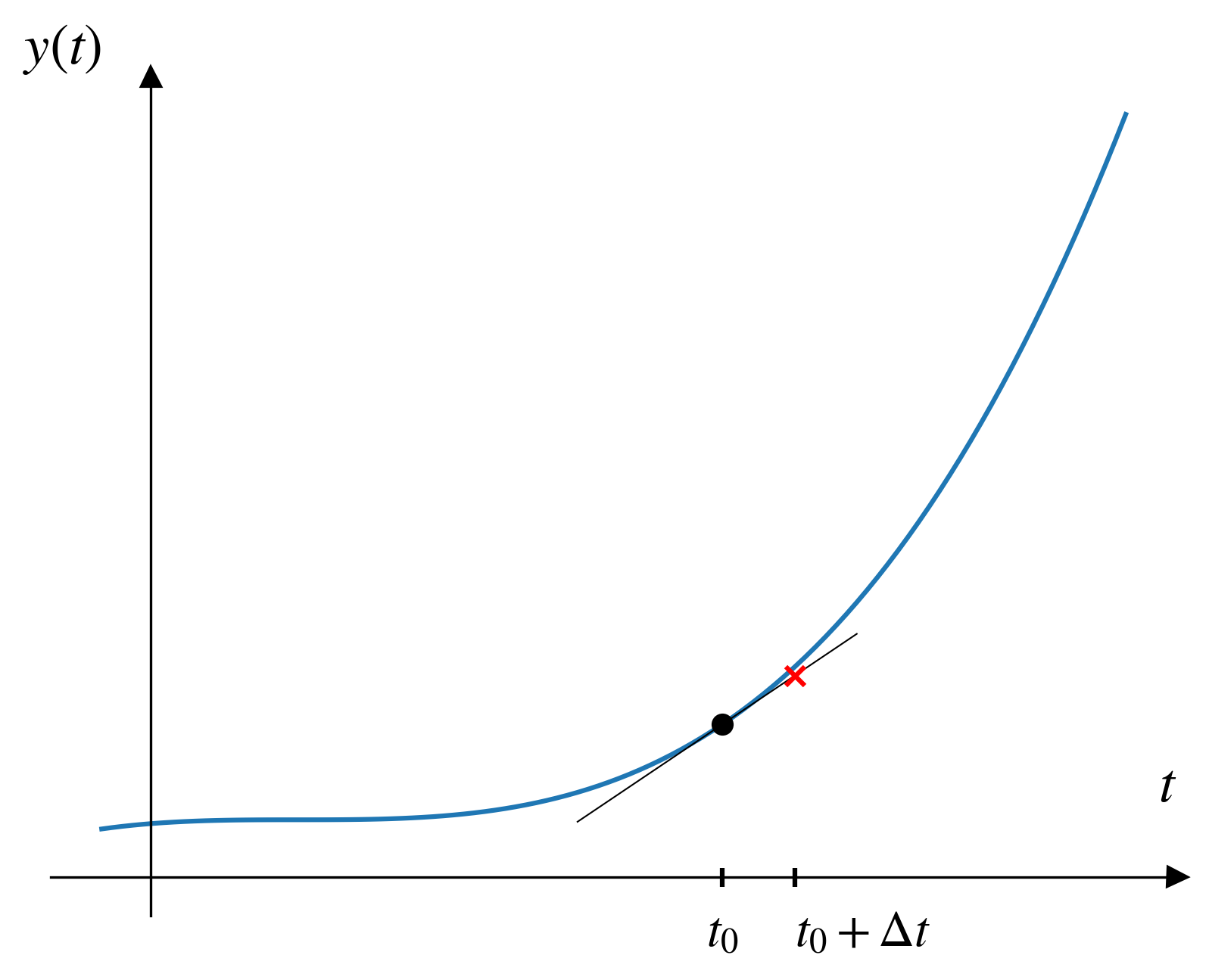
The key components
To solve a differential equation with Euler’s method we need to start with two things:
- A function describing the derivative of our parameter of interest
- An initial condition
Euler algorithm
Given:
- A function for the derivative: \(f(t, y) = \frac{dy}{dt}\)
- An initial condition: \(y(t_0) = y_0\)
- Step size: \(\Delta t\)
For \(n = 1, 2, 3 \ldots\): \[t_{n+1} = t_n + \Delta t\] \[y_{n+1} = y_n + \Delta t \cdot f(t_n, y_n)\]
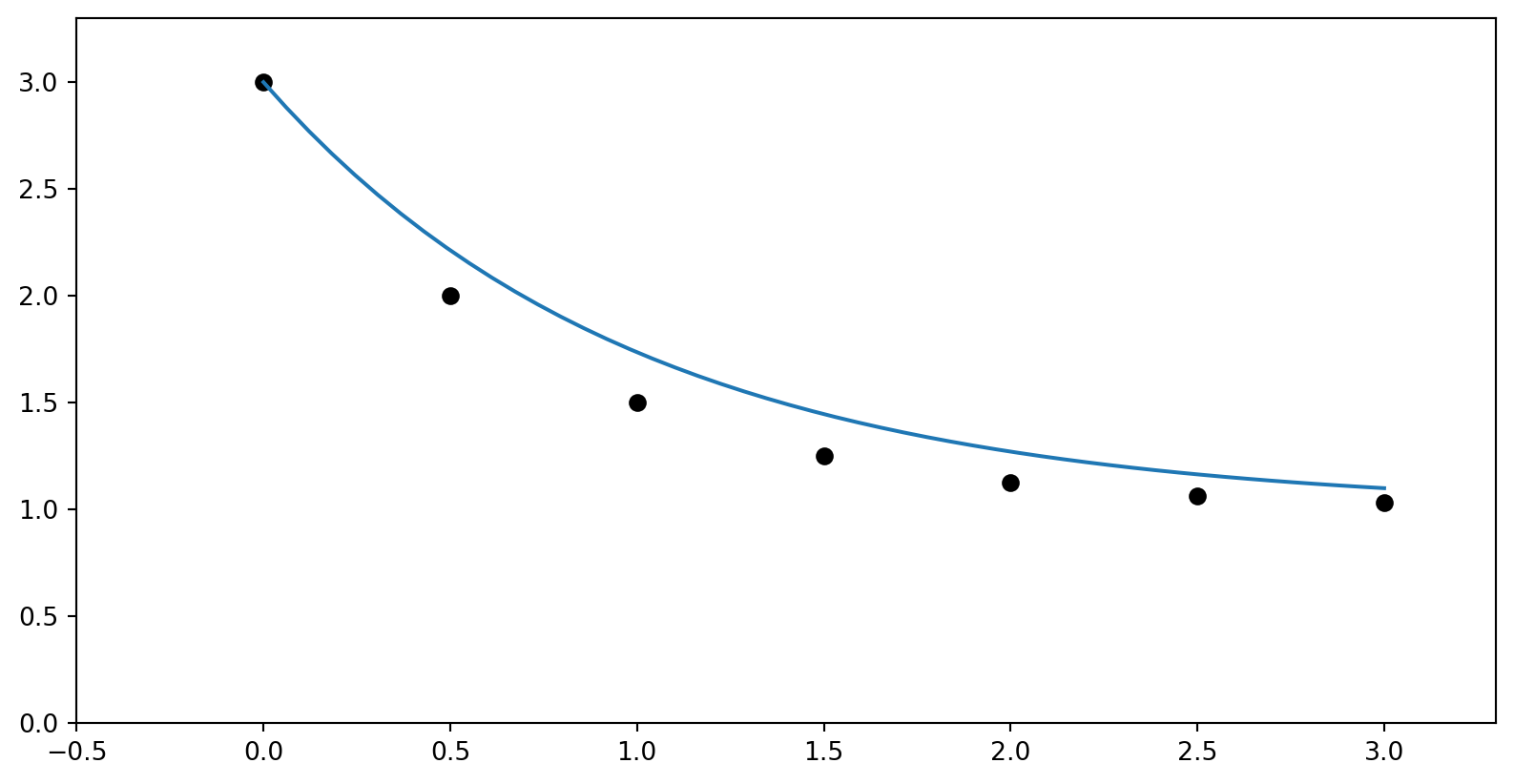
Example Problem
Use the differential equation and initial condition below to find \(y\) when \(t=2.5\):
\[y(t) = 1 - \frac{dy}{dt},\quad y(0) = 3\]
Let’s use Euler’s method with \(\Delta t = 0.5\) to approximate \(y(2.5)\).
Let’s rearrange the differential equation so we have a “function for the derivative”:
\[\frac{dy}{dt} = 1 - y(t)\]
Solution
Given:
\(y(0) = 3\)
\(\Delta t = 0.5\)
\(\frac{dy}{dt} = 1 - y(t)\)
Euler equations:
\(t_{n+1} = t_n + \Delta t\)
\(y_{n+1} = y_n + \Delta t \cdot \frac{dy}{dt}\)
0 0.0 3.0 -2.0 1 0.5 2.0 -1.0 2 1.0 1.5 -0.5 3 1.5 1.25 -0.25 4 2.0 1.125 -0.125 5 2.5 1.0625 -0.0625y(2.5) is approximately 1.0625Visualizing the solution