Error definitions
TME 310 - Computational Physical Modeling
University of Washington Tacoma
Absolute and relative error (true)
The true absolute error, \(E_t\), is the difference between the true value and our approximation:
\[E_t = \text{true} - \text{approx}\]
The true relative error, \(\epsilon_t\) is:
\[\epsilon_t = \frac{\text{true} - \text{approx}}{\text{true}} (\text{often}\times 100\%)\]
\[\epsilon_t = \frac{E_t}{\text{true}} (\text{often}\times 100\%)\]
Absolute and relative error (approx.)
We rarely know the true value (why approximate what we know exactly?)
The approximate absolute error, \(E_a\) is:
\[E_a = \text{current approx} - \text{previous approx}\]
The approximate relative error, \(\epsilon_a\) is:
\[\epsilon_a = \frac{E_a}{\text{current approx}} (\text{often}\times 100\%)\]
Key differences
With approximate errors:
- We do not need to know the true value
- We must perform the calculation iteratively
- We assume that our solution converges
- If it doesn’t we likely have a problem with our model.
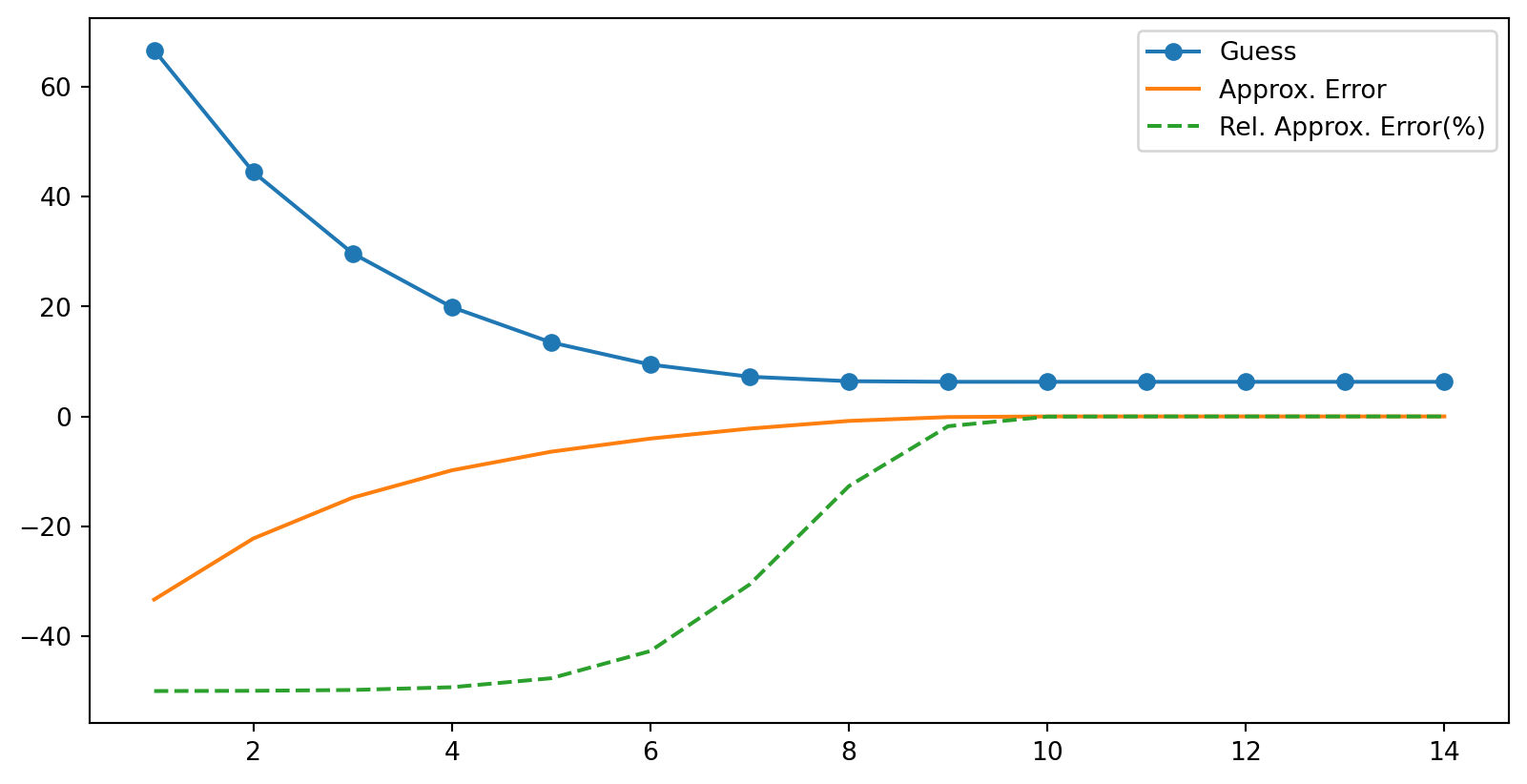
Example - \(\sqrt[3]{250}\)
Iter. Guess E_a e_a(%)
---------------------------------------
1 66.675000 -33.3250 -49.982 44.468745 -22.2063 -49.943 29.687972 -14.7808 -49.794 19.886530 -9.8014 -49.295 13.468404 -6.4181 -47.656 9.438331 -4.0301 -42.707 7.227688 -2.2106 -30.598 6.413676 -0.8140 -12.699 6.301622 -0.1121 -1.7810 6.299606 -0.0020 -0.03Example - cubed root of 250 (plot)
Visualize the algorithm’s convergence with a plot
Which to use?
Think about each scenario critically.
Often best to use an approximate relative error method (\(\epsilon_a\)) when:
- Target unknown
- Not converging near zero
When converging to zero (known target), true absolute error method often best.