TME 310 - Computational Physical Modeling
Modeling Framework
University of Washington Tacoma
Modeling Framework
The modeling framework we’ll use in this course consists of four elements and four activities.
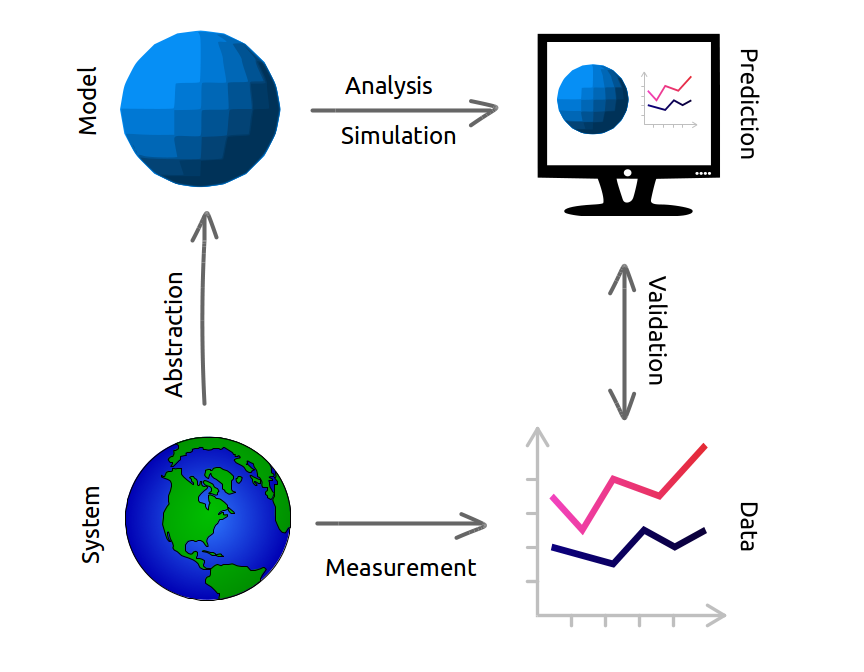
Modeling Framework
Elements
- System
- The real world.
- Model
- A simplified representation of the system.
- Prediction
- How the model says the system will behave
- Data
- Record of the system’s behavior.

Modeling Framework
Activities
- Abstraction
- Removing details to create a simpler representation of something
- Analysis (or simulation)
- Performing calculations with the model
- Validation
- Comparing predicted and actual behavior of a system
- Measurement
- Recording observations of the system.

An Example
Lorne has a box of chocolates he doesn’t want to share with his family. He decides to hide them in his garage next to his air compressor. He knows that air heats up when it’s compressed and that the chocolates will melt at 42 degrees Celsius. He recalls that some old French guy came up with something called the ideal gas law:
\[PV = nRT\]
(\(P\) = pressure, \(V\) = volume, \(n\) = moles, \(R\) = 6.023E+23, \(T\) = temperature). Punching some best guess numbers into his calculator, he estimates the air compressor will get up to 34 degrees Celsius when he uses it. His chocolates should be safe! After he next uses the air compressor, Lorne checks in on his precious chocolates and discovers a puddle of delicious goo. As he drizzles the remains over a bowl of ice cream, Lorne thinks Hmm… I guess this got a bit warmer than 34 degrees.

An Example
Lorne has a box of chocolates he doesn’t want to share with his family. He decides to hide them in his garage next to his air compressor. He knows that air heats up when it’s compressed and that the chocolates will melt at 42 degrees Celsius. He recalls that some old French guy came up with something called the ideal gas law:
\[PV = nRT\]
(\(P\) = pressure, \(V\) = volume, \(n\) = moles, \(R\) = 6.023E+23, \(T\) = temperature). Punching some best guess numbers into his calculator, he estimates the air compressor will get up to 34 degrees Celsius when he uses it. His chocolates should be safe! After he next uses the air compressor, Lorne checks in on his precious chocolates and discovers a puddle of delicious goo. As he drizzles the remains over a bowl of ice cream, Lorne thinks Hmm… I guess this got a bit warmer than 34 degrees.

- System
- The real world.
An Example
Lorne has a box of chocolates he doesn’t want to share with his family. He decides to hide them in his garage next to his air compressor. He knows that air heats up when it’s compressed and that the chocolates will melt at 42 degrees Celsius. He recalls that some old French guy came up with something called the ideal gas law:
\[PV = nRT\]
(\(P\) = pressure, \(V\) = volume, \(n\) = moles, \(R\) = 6.023E+23, \(T\) = temperature). Punching some best guess numbers into his calculator, he estimates the air compressor will get up to 34 degrees Celsius when he uses it. His chocolates should be safe! After he next uses the air compressor, Lorne checks in on his precious chocolates and discovers a puddle of delicious goo. As he drizzles the remains over a bowl of ice cream, Lorne thinks Hmm… I guess this got a bit warmer than 34 degrees.

- Abstraction
- Removing details to create a simpler representation of something
An Example
Lorne has a box of chocolates he doesn’t want to share with his family. He decides to hide them in his garage next to his air compressor. He knows that air heats up when it’s compressed and that the chocolates will melt at 42 degrees Celsius. He recalls that some old French guy came up with something called the ideal gas law:
\[PV = nRT\]
(\(P\) = pressure, \(V\) = volume, \(n\) = moles, \(R\) = 6.023E+23, \(T\) = temperature). Punching some best guess numbers into his calculator, he estimates the air compressor will get up to 34 degrees Celsius when he uses it. His chocolates should be safe! After he next uses the air compressor, Lorne checks in on his precious chocolates and discovers a puddle of delicious goo. As he drizzles the remains over a bowl of ice cream, Lorne thinks Hmm… I guess this got a bit warmer than 34 degrees.

- Model
- A simplified representation of the system.
An Example
Lorne has a box of chocolates he doesn’t want to share with his family. He decides to hide them in his garage next to his air compressor. He knows that air heats up when it’s compressed and that the chocolates will melt at 42 degrees Celsius. He recalls that some old French guy came up with something called the ideal gas law:
\[PV = nRT\]
(\(P\) = pressure, \(V\) = volume, \(n\) = moles, \(R\) = 6.023E+23, \(T\) = temperature). Punching some best guess numbers into his calculator, he estimates the air compressor will get up to 34 degrees Celsius when he uses it. His chocolates should be safe! After he next uses the air compressor, Lorne checks in on his precious chocolates and discovers a puddle of delicious goo. As he drizzles the remains over a bowl of ice cream, Lorne thinks Hmm… I guess this got a bit warmer than 34 degrees.

- Analysis (or simulation)
- Performing calculations with the model
An Example
Lorne has a box of chocolates he doesn’t want to share with his family. He decides to hide them in his garage next to his air compressor. He knows that air heats up when it’s compressed and that the chocolates will melt at 42 degrees Celsius. He recalls that some old French guy came up with something called the ideal gas law:
\[PV = nRT\]
(\(P\) = pressure, \(V\) = volume, \(n\) = moles, \(R\) = 6.023E+23, \(T\) = temperature). Punching some best guess numbers into his calculator, he estimates the air compressor will get up to 34 degrees Celsius when he uses it. His chocolates should be safe! After he next uses the air compressor, Lorne checks in on his precious chocolates and discovers a puddle of delicious goo. As he drizzles the remains over a bowl of ice cream, Lorne thinks Hmm… I guess this got a bit warmer than 34 degrees.

- Prediction
- How the model says the system will behave
An Example
Lorne has a box of chocolates he doesn’t want to share with his family. He decides to hide them in his garage next to his air compressor. He knows that air heats up when it’s compressed and that the chocolates will melt at 42 degrees Celsius. He recalls that some old French guy came up with something called the ideal gas law:
\[PV = nRT\]
(\(P\) = pressure, \(V\) = volume, \(n\) = moles, \(R\) = 6.023E+23, \(T\) = temperature). Punching some best guess numbers into his calculator, he estimates the air compressor will get up to 34 degrees Celsius when he uses it. His chocolates should be safe! After he next uses the air compressor, Lorne checks in on his precious chocolates and discovers a puddle of delicious goo. As he drizzles the remains over a bowl of ice cream, Lorne thinks Hmm… I guess this got a bit warmer than 34 degrees.

- Measurement
- Recording observations of the system.
An Example
Lorne has a box of chocolates he doesn’t want to share with his family. He decides to hide them in his garage next to his air compressor. He knows that air heats up when it’s compressed and that the chocolates will melt at 42 degrees Celsius. He recalls that some old French guy came up with something called the ideal gas law:
\[PV = nRT\]
(\(P\) = pressure, \(V\) = volume, \(n\) = moles, \(R\) = 6.023E+23, \(T\) = temperature). Punching some best guess numbers into his calculator, he estimates the air compressor will get up to 34 degrees Celsius when he uses it. His chocolates should be safe! After he next uses the air compressor, Lorne checks in on his precious chocolates and discovers a puddle of delicious goo. As he drizzles the remains over a bowl of ice cream, Lorne thinks Hmm… I guess this got a bit warmer than 34 degrees.

- Data
- Record of the system’s behavior.
An Example
Lorne has a box of chocolates he doesn’t want to share with his family. He decides to hide them in his garage next to his air compressor. He knows that air heats up when it’s compressed and that the chocolates will melt at 42 degrees Celsius. He recalls that some old French guy came up with something called the ideal gas law:
\[PV = nRT\]
(\(P\) = pressure, \(V\) = volume, \(n\) = moles, \(R\) = 6.023E+23, \(T\) = temperature). Punching some best guess numbers into his calculator, he estimates the air compressor will get up to 34 degrees Celsius when he uses it. His chocolates should be safe! After he next uses the air compressor, Lorne checks in on his precious chocolates and discovers a puddle of delicious goo. As he drizzles the remains over a bowl of ice cream, Lorne thinks Hmm… I guess this got a bit warmer than 34 degrees.

- Validation
- Comparing predicted and actual behavior of a system
Another Example
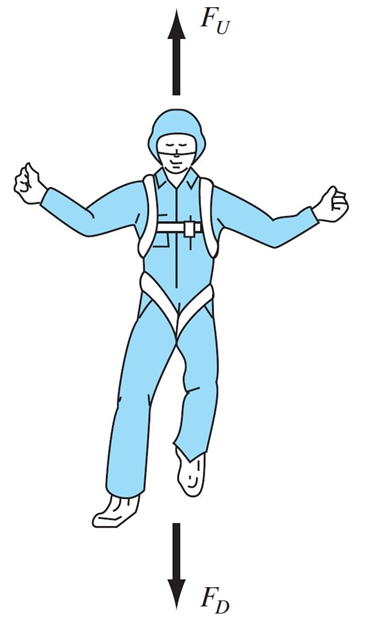
Parachute Problem
What’s the terminal velocity of someone falling with a parachute? (this is our system)
Let’s say we have a model for this problem:
\[\frac{dv}{dt} = g -\frac{c}{m}v\]
where \(g\) is gravitational acceleration, \(c\) is a drag coefficient, \(m\) is the parachutist’s mass, and \(v\) is their velocity.
The abstraction was done for us!
The model is a differential equation with the solution
\[ v(t) = \frac{gm}{c}(1 - e^{ct/m})\]
Another Example
If we can get our model into Python, we can easily do some analysis to make a prediction about the terminal velocity.
Let’s move over to a Jupyter Notebook to do that.
But first…
What about measuring data for us to do the validiation step?

Another Example
Validation options
As we saw with abstraction, we don’t have to do every step of this problem ourselves.
If we have reliable information about how a system behaves, we can perform validation (or at least partial validation) of our model.
For example, no matter what the actual terminal velocity is, we probably know enough to expect:
- Velocity should increase linearly without any drag coefficient.
- Things fall downwards.
- At “terminal velocity” things fall at a constant rate
